Question

17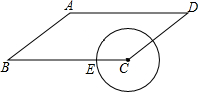．如图，已知在平行四边形ABCD中，AB=5，BC=8，cosB=$\frac{4}{5}$，点E是BC边上的动点，当以CE为半径的⊙C与边AD有两个交点时，半径CE的取值范围是（　　）

• A． 0＜CE≤8
• B． 0＜CE≤5
• C． 3＜CE≤8
• D． 3＜CE≤5

Answer 1

分析 过A作AM⊥BC于N，CN⊥AD于N，根据平行四边形的性质求出AD∥BC，AB=CD=5，求出AM、CN、AC、CD的长，即可得出符合条件的情况．

解答 解：如图，过A作AM⊥BC于N，CN⊥AD于N，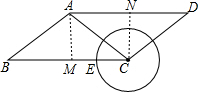

∵四边形ABCD是平行四边形，
∴AD∥BC，AB=CD=5，
∴AM=CN，
∵AB=5，cosB=$\frac{4}{5}=\frac{BM}{AB}$，
∴BM=4，
∵BC=8，
∴CM=4=BC，
∵AM⊥BC，
∴AC=AB=5，
由勾股定理得：AM=CN=$\sqrt{A{C}^{2}-C{M}^{2}}$=3，
∴当以CE为半径的圆C与边AD有两个交点时，半径CE的取值范围是3＜CE≤5，
故选：D．

点评 本题考查了直线和圆的位置关系，勾股定理，平行四边形的性质的应用，能求出符合条件的所有情况是解此题的关键，此题综合性比较强，有一定的难度．