题目内容
7.关于x的方程$\frac{ax+1}{a-2}$=-1的解是正数,则a的取值范围是0<a<1.分析 根据解分式方程的步骤,可得分式方程的解,根据分式方程的解是正数,可得答案.
解答 解:方程$\frac{ax+1}{a-2}$=-1的解是:x=$\frac{-a+1}{a}$,
∵方程的解是正数,
∴$\frac{-a+1}{a}>0$,
当a>0时,即-a+1>0,解得:a<1,
∴0<a<1,
当a<0时,即-a+1<0,解得:a>1,舍去;
∴a的取值范围为:0<a<1.
点评 本题考查了分式方程的解,解决本题的关键是解分式方程.注意分式方程中分母不为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.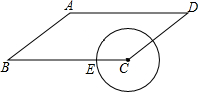 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 3<CE≤8 | D. | 3<CE≤5 |
17.下列说法正确的是( )
| A. | 方差反映了一组数据的分散或波动的程度 | |
| B. | 数据1,5,3,7,10的中位数是3 | |
| C. | 任何一组数据的平均数和众数都不相等 | |
| D. | 调查一批灯泡的使用寿命适合用全面调查方式 |
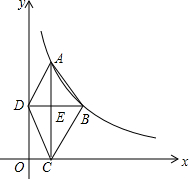 如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.
如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.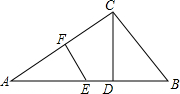 如图,在Rt△ABC中,∠ACB=90°,AF=4,EF⊥AC交AB于E,CD⊥AB,垂足为D.若CD=4,EF=3.则ED=$\frac{1}{3}$,BC=5,AB=$\frac{25}{3}$.
如图,在Rt△ABC中,∠ACB=90°,AF=4,EF⊥AC交AB于E,CD⊥AB,垂足为D.若CD=4,EF=3.则ED=$\frac{1}{3}$,BC=5,AB=$\frac{25}{3}$.