题目内容
12.在下列各数0.51525354…、0、$0.\stackrel{•}2$、3π、$\frac{22}{7}$、$\root{3}{9}$、$\frac{131}{11}$、$\sqrt{27}$中,无理数有0.51525354…、3π、$\root{3}{9}$、$\sqrt{27}$.分析 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.
解答 解:0是有理数;
∵$0.\stackrel{•}2$、$\frac{22}{7}=3.\stackrel{•}{1}4285\stackrel{•}{7}$、$\frac{131}{11}=11.\stackrel{•}{9}\stackrel{•}{0}$都是循环小数,
∴0、$0.\stackrel{•}2$、$\frac{131}{11}$都是有理数;
∵0.51525354…、3π、$\root{3}{9}$、$\sqrt{27}$都是无限不循环小数,
∴0.51525354…、3π、$\root{3}{9}$、$\sqrt{27}$都是无理数;
∴无理数有:0.51525354…、3π、$\root{3}{9}$、$\sqrt{27}$.
故答案为:0.51525354…、3π、$\root{3}{9}$、$\sqrt{27}$.
点评 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
17.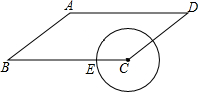 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 3<CE≤8 | D. | 3<CE≤5 |
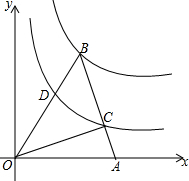 如图,坐标系中,AB⊥x轴于A点,双曲线y=$\frac{{k}_{1}}{x}$过点B,反比例函数y=$\frac{{k}_{2}}{x}$过C,D点且OD=BC,已知B(2,3),则D点坐标为($\frac{-\sqrt{13}+7}{3}$,$\frac{-\sqrt{13}+7}{2}$).
如图,坐标系中,AB⊥x轴于A点,双曲线y=$\frac{{k}_{1}}{x}$过点B,反比例函数y=$\frac{{k}_{2}}{x}$过C,D点且OD=BC,已知B(2,3),则D点坐标为($\frac{-\sqrt{13}+7}{3}$,$\frac{-\sqrt{13}+7}{2}$).
 如图,在等腰三角形ABC中,∠BAC=90°,点A、B分别在x轴正半轴上和y轴的负半轴上,点A的坐标为(3,0),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C(7,n),则k的值为( )
如图,在等腰三角形ABC中,∠BAC=90°,点A、B分别在x轴正半轴上和y轴的负半轴上,点A的坐标为(3,0),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C(7,n),则k的值为( )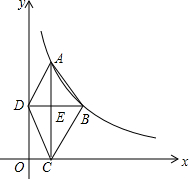 如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.
如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.