题目内容
6.解不等式组$\left\{\begin{array}{l}{3-(2x-1)≥5x+4}\\{\frac{x}{2}-3≤2x}\end{array}\right.$,并将解集在数轴上表示出来.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{3-(2x-1)≥5x+4①}\\{\frac{x}{2}-3≤2x②}\end{array}\right.$
∵解不等式①得:x≤0,
解不等式②得:x≥-2,
∴不等式组的解集为-2≤x≤0,
在数轴上表示不等式组的解集为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
17.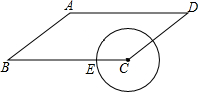 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 3<CE≤8 | D. | 3<CE≤5 |
1.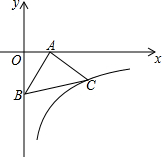 如图,在等腰三角形ABC中,∠BAC=90°,点A、B分别在x轴正半轴上和y轴的负半轴上,点A的坐标为(3,0),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C(7,n),则k的值为( )
如图,在等腰三角形ABC中,∠BAC=90°,点A、B分别在x轴正半轴上和y轴的负半轴上,点A的坐标为(3,0),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C(7,n),则k的值为( )
 如图,在等腰三角形ABC中,∠BAC=90°,点A、B分别在x轴正半轴上和y轴的负半轴上,点A的坐标为(3,0),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C(7,n),则k的值为( )
如图,在等腰三角形ABC中,∠BAC=90°,点A、B分别在x轴正半轴上和y轴的负半轴上,点A的坐标为(3,0),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C(7,n),则k的值为( )| A. | -21 | B. | 21 | C. | -9 | D. | 9 |
11.若将分式$\frac{a+b}{2ab}$中的字母a,b的值分别扩大到原来的2倍,则分式的值( )
| A. | 扩大到原来的2倍 | B. | 缩小到原来的$\frac{1}{2}$ | C. | 缩小到原来的$\frac{1}{4}$ | D. | 不变 |