题目内容
10.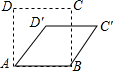 如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.
如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.
分析 过D′作D′M⊥AB于M,求出D′M,再根据平行四边形和矩形的面积公式求出即可.
解答 解:过D′作D′M⊥AB于M,如图所示.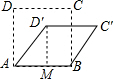
∵∠BAD′=45°,
∴△AMD′为等腰直角三角形,
∴D′M=$\frac{\sqrt{2}}{2}$AD′=$\frac{\sqrt{2}}{2}$AB,
∴S正方形ABCD=AB2,S菱形ABC′D′=AB•D′M=$\frac{\sqrt{2}}{2}$AB2,
∴正方形ABCD的面积与菱形ABC′D′的面积之比为1:$\frac{\sqrt{2}}{2}$=$\sqrt{2}$:1.
点评 本题考查了菱形的性质、等腰直角三角形、正方形和平行四边形的面积,求出菱形ABC′D′的高D′M是解题的关键.

练习册系列答案
相关题目
18.下列说法中,正确的个数有( )
①同位角相等
②三角形的高在三角形内部
③一个多边形的边数每增加一条,这个多边形的内角和就增加180°,
④两个角的两边分别平行,则这两个角相等.
①同位角相等
②三角形的高在三角形内部
③一个多边形的边数每增加一条,这个多边形的内角和就增加180°,
④两个角的两边分别平行,则这两个角相等.
| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
5.(1)填空
31-30=3(0 )×2
32-31=3(1 )×2
33-32=3(2 )×2
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立.
(3)计算:3+32+…+32017.
31-30=3(0 )×2
32-31=3(1 )×2
33-32=3(2 )×2
(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立.
(3)计算:3+32+…+32017.
15.反比例函数y=$\frac{1}{x}$经过( )象限.
| A. | 第一和第三 | B. | 第二和第四 | C. | 第一和第二 | D. | 第三和第四 |
20.平面内三条直线a、b、c,若a⊥b,b⊥c,则直线a、c的位置关系是( )
| A. | 垂直 | B. | 平行 | C. | 相交 | D. | 以上都不对 |