题目内容
20.平面直角坐标系中有函数y1、y2、y3,y1=ax2+bx+c(a≠0),y2=-x2+2x,y3=kx+b(k≠0),y1的图象向右平移2个单位,再向上平移1个单位后与y2的图象重合,y3经过y1与y轴的交点以及y2的顶点.(1)求y1和y3的表达式;
(2)当x≥0时,试比较y2与y3的大小;
(3)当x<m时,y1,y2,y3均随着x的增大而增大,求实数m的最大值.
分析 (1)根据y1、y2图象间的关系结合y2的函数表达式,即可得出y1的表达式,进而可找出y1与y轴的交点和y2的顶点,根据点的坐标利用待定系数法即可求出y1的表达式;
(2)画出y2与y3的函数图象,观察图象,即可得出结论;
(3)根据y1、y2、y3的表达式,找出它们的单增区间,由此即可得出实数m的最大值.
解答 解:(1)∵y1向右平移2个单位,向上平移1个单位得到y2,
∴y2向左平移2个单位,向下平移1个单位得到y1,
∵y2=-x2+2x,
∴y1=-(x+2)2+2(x+2)-1,
∴y1的表达式为y1=-x2-2x-1,
∴y1与y轴的交点为(0,-1).
∵y2=-x2+2x=-(x-1)2+1,
∴y2的顶点坐标为(1,1).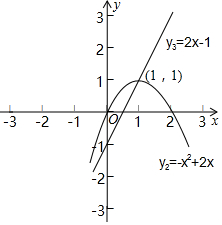
∵y3经过(0,-1)、(1,1),
∴$\left\{\begin{array}{l}{b=-1}\\{k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴y3的表达式为y3=2x-1.
(2)依照题意,画出函数y2、y3的图象,如图所示.
观察函数图象,可得:
当0≤x<1时,y2>y3;
当x=1时,y2=y3;
当x>1时,y2<y3.
(3)∵y1=-x2-2x-1=-(x+1)2,y2=-(x-1)2+1,y3=2x-1,
∴y1在x≤-1时随x的增大而增大,y2在x≤1时随x的增大而增大,y3一直都随x的增大而增大,
∴m≤-1时,y1,y2,y3均随着x的增大而增大,
∴m的最大值为-1.
点评 本题考查了二次函数与不等式、待定系数法求一次函数解析式、二次(一次)函数图象以及二次函数的性质,解题的关键是:(1)利用平移找出y1的表达式;(2)画出函数图象,利用数形结合解决问题;(3)找出三个函数的单增区间.

| A. | 4,5,10 | B. | 2,6,8 | C. | 3,4,5 | D. | 5,7,13 |
| A. | a3•a2=a6 | B. | a3-a2=a | C. | (-a3)2=a6 | D. | a6÷a2=a3 |
 如图,l1∥l2,∠1=110°,则∠2的度数是( )
如图,l1∥l2,∠1=110°,则∠2的度数是( )| A. | 70° | B. | 110° | C. | 120° | D. | 60° |
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
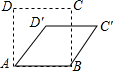 如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.
如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.