Question

9．感知：如图①，OC平分∠AOB，P是OC上任意一点，PM⊥OA于点M，PN⊥OB于点N，由三角形全等的判定方法“AAS”易证△OPM≌△OPN，得到角平分线的一条性质“角平分线上的点到这个角两边的距离相等”．
探究：如图②，在平面直角坐标系中，已知A（7，0），B（7，24），点D在线段AB上，OD平分∠AOB，求$\frac{AD}{OA}$的值．
应用：将图②中的∠AOB绕原点O顺时针旋转，使∠AOB的边OB落在第一象限的角平分线上，如图③，点P在∠AOB的平分线上，当点P的横、纵坐标均为整数时，OP长度的最小值为5$\sqrt{2}$．（可参考提供的网格求值）

Answer 1

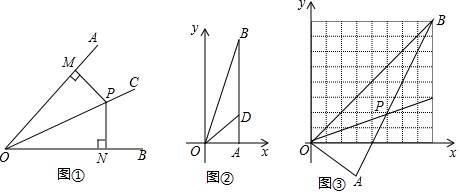
分析 （1）探究：如图②中，作DH⊥OB于H，Rt△ODH≌Rt△ODA，推出OH=OA=7，设DH=AD=x，在Rt△OAB中，OB=$\sqrt{{7}^{2}+2{4}^{2}}$=25，推出BH=OB-OH=25-7=18，在Rt△BHD中，根据BH²+DH²=BD²，推出18²+x²=（24-x）²，解方程即可解决问题．
（2）应用：如图③中，作BG⊥x轴于G，OP交BG于K，作KH⊥OB于H．由（1）可知tan∠BOP=tan∠POA=$\frac{3}{4}$=$\frac{HK}{OH}$，设HK=3m，OH=4m，则HK=BH=3m，BK=3$\sqrt{2}$m，由OB=8$\sqrt{2}$，推出OH+BH=8$\sqrt{2}$，即4m+3m=8$\sqrt{2}$，可得m=$\frac{8\sqrt{2}}{7}$，推出BK=$\frac{48}{7}$，推出KG=8-$\frac{48}{7}$=$\frac{8}{7}$，可得K（8，$\frac{8}{7}$），推出直线OK的解析式为y=$\frac{1}{7}$x，在直线OK寻找整数点P，即可解决问题．

解答 解：（1）探究：如图②中，作DH⊥OB于H，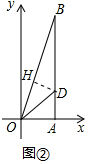

∵OD平分∠AOB，DH⊥OB，DA⊥OA，
∴DH=DA，
在Rt△ODH和Rt△ODA中，
$\left\{\begin{array}{l}{OD=OD}\\{DH=DA}\end{array}\right.$，
Rt△ODH≌Rt△ODA，
∴OH=OA=7，设DH=AD=x，
在Rt△OAB中，OB=$\sqrt{{7}^{2}+2{4}^{2}}$=25，
∴BH=OB-OH=25-7=18，
在Rt△BHD中，∵BH²+DH²=BD²，
∴18²+x²=（24-x）²，
∴x=$\frac{21}{4}$，
∴$\frac{AD}{OA}$=$\frac{\frac{21}{4}}{7}$=$\frac{3}{4}$．

（2）应用：如图③中，作BG⊥x轴于G，OP交BG于K，作KH⊥OB于H．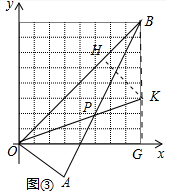

∵B（8，8），B（8，0），
由（1）可知tan∠BOP=tan∠POA=$\frac{3}{4}$=$\frac{HK}{OH}$，设HK=3m，OH=4m，则HK=BH=3m，BK=3$\sqrt{2}$m，
∵OB=8$\sqrt{2}$，
∴OH+BH=8$\sqrt{2}$，即4m+3m=8$\sqrt{2}$，
∴m=$\frac{8\sqrt{2}}{7}$，
∴BK=$\frac{48}{7}$，
∴KG=8-$\frac{48}{7}$=$\frac{8}{7}$，
∴K（8，$\frac{8}{7}$），
∴直线OK的解析式为y=$\frac{1}{7}$x，
∵点P在直线OK上，点P的横、纵坐标均为整数，
∴当P（7，1）时，OP长度的值最小，最小值=$\sqrt{{7}^{2}+{1}^{2}}$=$\sqrt{50}$=5$\sqrt{2}$．
故答案为5$\sqrt{2}$．

点评 本题考查相似三角形的判定和性质、角平分线性质定理、整数点、勾股定理、锐角三角函数等整数，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，应用中求出直线OP的解析式是突破点，属于中考压轴题．