题目内容
8.因式分解:(m-4)(m+1)+3m=(m+2)(m-2).分析 首先去括号,进而合并同类项,再利用平方差公式分解因式即可.
解答 解:(m-4)(m+1)+3m
=m2-3m-4+3m
=m2-4
=(m+2)(m-2).
故答案为:(m+2)(m-2).
点评 此题主要考查了公式法分解因式,正确掌握平方差公式是解题关键.

练习册系列答案
相关题目
19.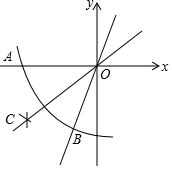 如图,在平面直角坐标系中,依下列步骤尺规作图,并保留作图痕迹:
如图,在平面直角坐标系中,依下列步骤尺规作图,并保留作图痕迹:
步骤1:以点O为圆心,任意长为半径画弧,与x轴负半轴交于点A,与直线y=$\sqrt{3}$x交于点B(点B在第三象限):
步骤2:分别以点A,B为圆心,以大于$\frac{1}{2}$AB长为半径画弧,两弧交于点C.
则直线OC的函数解析式为( )
 如图,在平面直角坐标系中,依下列步骤尺规作图,并保留作图痕迹:
如图,在平面直角坐标系中,依下列步骤尺规作图,并保留作图痕迹:步骤1:以点O为圆心,任意长为半径画弧,与x轴负半轴交于点A,与直线y=$\sqrt{3}$x交于点B(点B在第三象限):
步骤2:分别以点A,B为圆心,以大于$\frac{1}{2}$AB长为半径画弧,两弧交于点C.
则直线OC的函数解析式为( )
| A. | y=$\frac{\sqrt{3}}{2}$x | B. | y=-$\frac{\sqrt{3}}{2}$x | C. | y=$\frac{\sqrt{3}}{3}$x | D. | y=-$\frac{\sqrt{3}}{3}$x |
16. 如图,已知点C在线段AB上,点C所表示的数为m,则-m不可能是( )
如图,已知点C在线段AB上,点C所表示的数为m,则-m不可能是( )
 如图,已知点C在线段AB上,点C所表示的数为m,则-m不可能是( )
如图,已知点C在线段AB上,点C所表示的数为m,则-m不可能是( )| A. | 2 | B. | $\frac{3}{2}$ | C. | -1 | D. | -3 |
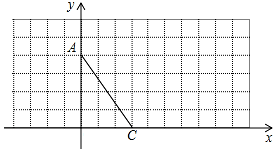 如图,在直角坐标系中,A(0,4)、C(3,0),
如图,在直角坐标系中,A(0,4)、C(3,0),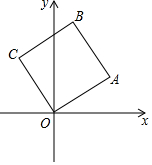 已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).
已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).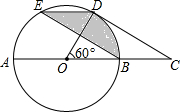 如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB.
如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB. 如图,一透明的圆柱体玻璃杯,从内部测得底部直径为6cm,杯深8cm.今有一根长为16cm的吸管如图放入杯中,露在杯口外的长度为h,则h的变化范围是:6cm≤h≤8cm.
如图,一透明的圆柱体玻璃杯,从内部测得底部直径为6cm,杯深8cm.今有一根长为16cm的吸管如图放入杯中,露在杯口外的长度为h,则h的变化范围是:6cm≤h≤8cm.