题目内容
8.在△ABC中,AB=13,BC=14.(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为84;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.
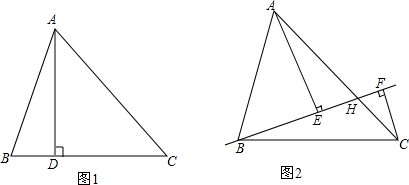
分析 (1)先由勾股定理求得AD=12,然后利用三角形的面积公式求解即可;
(2)依据SABC=SABH+S△BHC可知$\frac{1}{2}BH•AE+\frac{1}{2}BH•CF=84$,然后将BH=x,AE=m,CF=n代入整理即可.
解答 解:(1)在Rt△ABD中,AB=13,BD=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12.
∵BC=14,
∴${S}_{△ABC}=\frac{1}{2}BC•AD$=$\frac{1}{2}×14×12$=84.
故答案为:84.
(2)∵SABC=SABH+S△BHC,
∴$\frac{1}{2}BH•AE+\frac{1}{2}BH•CF=84$.
∴xm+xn=168.
∴m+n=$\frac{168}{x}$
∵AD=12,DC=14-5=9,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=15.
∵m+n与x成反比,
∴当BH⊥AC时,m+n有最大值.
∴(m+n)BH=AC•BH.
∴m+n=AC=15.
∵m+n与x成反比,
∴当BH值最大时,m+n有最小值.
∴当点H与点C重合时m+n有最小值.
∴m+n=$\frac{168}{14}$=∵$\frac{1}{2}AC•BH=84$,
∴m+n=12.
∴m+n的最大值为15,最小值为12.
点评 本题主要考查的是三角形的面积、勾股定理的应用,依据SABC=SABH+S△BHC得到m、n、x的关系式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
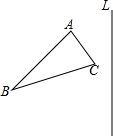 已知,△ABC和直线L如图所示,求作△A′B′C′,使图△A′B′C′和△ABC关于直线L对称,其中A、B、C点对称点分别为A′、B′、C′(尺规作图).
已知,△ABC和直线L如图所示,求作△A′B′C′,使图△A′B′C′和△ABC关于直线L对称,其中A、B、C点对称点分别为A′、B′、C′(尺规作图). 已知:如图,正方形ABCD中,点E在边CD上,点F在边AD上,DE=DF,AE与CF交于G,若AB=4,DG=$\sqrt{2}$,则线段GE的长是$\frac{\sqrt{10}}{3}$.
已知:如图,正方形ABCD中,点E在边CD上,点F在边AD上,DE=DF,AE与CF交于G,若AB=4,DG=$\sqrt{2}$,则线段GE的长是$\frac{\sqrt{10}}{3}$.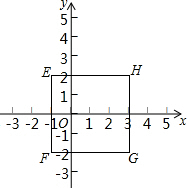 如图,在平面直角坐标系中正方形EFGH的顶点E、H、G的坐标分别是(-1,2),(3,2),(3,-2),则点F的坐标是(-1,-2).
如图,在平面直角坐标系中正方形EFGH的顶点E、H、G的坐标分别是(-1,2),(3,2),(3,-2),则点F的坐标是(-1,-2). 如图:已知直线m:y=2x和直线n:y=kx+10相交于点A,A点横坐标是2.
如图:已知直线m:y=2x和直线n:y=kx+10相交于点A,A点横坐标是2.