题目内容
3. 如图:已知直线m:y=2x和直线n:y=kx+10相交于点A,A点横坐标是2.
如图:已知直线m:y=2x和直线n:y=kx+10相交于点A,A点横坐标是2.(1)求直线n的表达式;
(2)求直线n与x轴交点B坐标;
(3)求△ABO的面积.
分析 (1)把x=2代入y=2x得出y=4,再把x=2,y=4代入y=kx+10解答即可;
(2)根据(1)中的解析式把y=0代入得出点B的坐标;
(3)根据三角形的面积公式解答即可.
解答 解:(1)把x=2代入y=2x,可得:y=4,
把x=2,y=4代入y=kx+10,可得:4=2k+10,
解得:k=-3,
所以直线n的表达式为:y=-3x+10;
(2)把y=0代入y=-3x+10,可得-3x+10=0,
解得:x=$\frac{10}{3}$,
所以点B($\frac{10}{3}$,0);
(3)S=$\frac{1}{2}×\frac{10}{3}×4=\frac{20}{3}$.
点评 本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2相交,则交点坐标同时满足两个解析式.也考查了待定系数法求函数解析式.

练习册系列答案
相关题目
13. 如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.
如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.
 如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.
如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.| A. | ① | B. | ② | C. | ③ | D. | ①和② |
14.已知正比例函数y=kx(k≠0)的图象经过点(-2,1),则正比例函数的解析式为( )
| A. | y=2x | B. | y=-2x | C. | y=-$\frac{1}{2}x$ | D. | y=$\frac{1}{2}x$ |
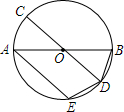 如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.
如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.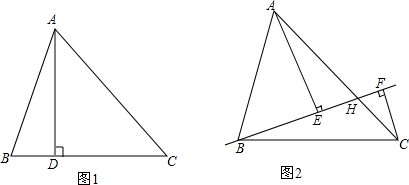
 如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.