题目内容
19. 已知:如图,正方形ABCD中,点E在边CD上,点F在边AD上,DE=DF,AE与CF交于G,若AB=4,DG=$\sqrt{2}$,则线段GE的长是$\frac{\sqrt{10}}{3}$.
已知:如图,正方形ABCD中,点E在边CD上,点F在边AD上,DE=DF,AE与CF交于G,若AB=4,DG=$\sqrt{2}$,则线段GE的长是$\frac{\sqrt{10}}{3}$.
分析 连接BG,先证B、G、D三点共线;然后利用平行线分线段成比例可求出DE,进而利用勾股定理求出AE的长度,GE自然求出.
解答 解:连接BG,如图,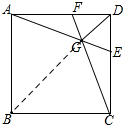
在△AED和△CFD中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDF}\\{DE=DF}\end{array}\right.$,
∴△AED≌△CFD(SAS),
∴∠DAG=∠DCG,∠AED=∠CFD,
∴∠AFG=∠CEG,
在△AFG和△CEG中,
$\left\{\begin{array}{l}{∠AFG=∠CEG}\\{AF=CE}\\{∠FAG=∠ECG}\end{array}\right.$,
∴△AFG≌△CEG(ASA),
∴AG=CG,
在△ADG和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{AG=CG}\\{DG=DG}\end{array}\right.$,
∴△ADG≌△CDG(SSS),
∴∠ADG=∠CDG,
∴B、G、D三点共线,
∵AB=4,
∴BD=4$\sqrt{2}$,
∵DG=$\sqrt{2}$,
∴BG=3$\sqrt{2}$,
∴$\frac{DE}{AB}=\frac{DG}{BG}=\frac{GE}{AG}=\frac{1}{3}$,
∴DE=$\frac{4}{3}$,
∴AE=$\frac{4\sqrt{10}}{3}$,
GE=$\frac{1}{4}AE=\frac{\sqrt{10}}{3}$.
故答案为:$\frac{\sqrt{10}}{3}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、平行线分线段成比例、相似三角形的判定与性质、勾股定理等知识点,难度中等.证明B、G、D三点共线是解决本题的突破口和关键所在.

| A. | y=2x | B. | y=-2x | C. | y=-$\frac{1}{2}x$ | D. | y=$\frac{1}{2}x$ |
| A. | $\sqrt{-a}$ | B. | -$\sqrt{a}$ | C. | -$\sqrt{-a}$ | D. | $\sqrt{a}$ |
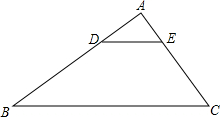 如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求:
如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求: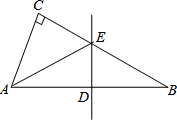 在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若∠CAE=30°,求∠AED的度数.
在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若∠CAE=30°,求∠AED的度数.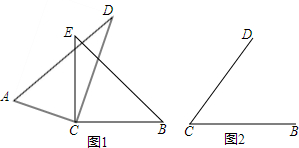
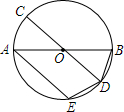 如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.
如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.