题目内容
18.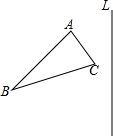 已知,△ABC和直线L如图所示,求作△A′B′C′,使图△A′B′C′和△ABC关于直线L对称,其中A、B、C点对称点分别为A′、B′、C′(尺规作图).
已知,△ABC和直线L如图所示,求作△A′B′C′,使图△A′B′C′和△ABC关于直线L对称,其中A、B、C点对称点分别为A′、B′、C′(尺规作图).
分析 分别过各点向直线l作垂线,再分别以垂足为圆心,以垂足到各点的距离为半径画圆,此圆与直线的交点即为各点关于直线l的对称点,再顺次连接即可.
解答  解:如图所示,
解:如图所示,
①过点A作直线AD⊥l于点D,以点D为圆心,AD为半径画圆交直线AD于点A′;
②过点C作直线CE⊥l于点E,以点E为圆心,CE为半径画圆交直线CE于点C′;
③过点B作直线BF⊥l于点F,以点F为圆心,BF为半径画圆交直线BF于点B′,再顺次连接各点即可.
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
相关题目
6.在实数:-(-3.14159),1.010010001…,-(-1)2013,$-|{-\frac{3}{4}}|$,$4.\stackrel{•}2\stackrel{•}1$,$\frac{π}{3}$,$\frac{22}{7}$中,正分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13. 如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.
如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.
 如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.
如图,一块三角形玻璃碎成了三块,现要去玻璃店配一块完全一样的玻璃,那么最好带( )去.| A. | ① | B. | ② | C. | ③ | D. | ①和② |
3.如果规定收入为正,支出为负.收入500元记作+500元,那么支出400元应记作( )
| A. | -500元 | B. | -400元 | C. | 500元 | D. | 400元 |
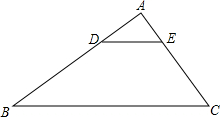 如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求:
如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求: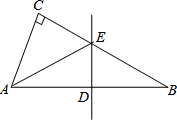 在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若∠CAE=30°,求∠AED的度数.
在△ABC中,∠C=90°,DE垂直平分斜边AB,且分别交AB、BC于D、E,若∠CAE=30°,求∠AED的度数.