题目内容
7. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | 2$\sqrt{10}$ | B. | 8 | C. | 2$\sqrt{17}$ | D. | 10 |
分析 根据平面内线段最短,构建直角三角形,解直角三角形即可.
解答  解:如图,过点作CO⊥AB于O,延长BO到C',使OC'=OC,连接MC',交AB于P,
解:如图,过点作CO⊥AB于O,延长BO到C',使OC'=OC,连接MC',交AB于P,
此时MC'=PM+PC'=PM+PC的值最小,
连接AC',
∵CO⊥AB,AC=BC,∠ACB=90°,
∴∠ACO=$\frac{1}{2}$×90°=45°,
∵CO=OC',CO⊥AB,
∴AC'=CA=AM+MC=8,
∴∠OC'A=∠OCA=45°,
∴∠C'AC=90°,
∴C'A⊥AC,
∴MC′=$\sqrt{A{M}^{2}+A{C}^{2}}$=$\sqrt{{2}^{2}+{8}^{2}}$=2$\sqrt{17}$,
∴PC+PM的最小值为2$\sqrt{17}$.
故选C.
点评 考查了线路最短的问题,确定动点P为何位置时,使PC+PM的值最小是关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8. 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P在直线OB上运动且满足∠APQ=90°,PQ交x轴于点C.点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,则PA:PC=( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\frac{{\sqrt{15}}}{5}$或$\frac{{\sqrt{15}}}{3}$ | D. | 以上都不对 |
6.下列去括号不正确的是( )
| A. | (a+$\frac{1}{2}$b)-(-$\frac{1}{3}$c+$\frac{2}{7}$)=a+$\frac{1}{2}$b+$\frac{1}{3}c$-$\frac{2}{7}$ | B. | m+(-n+a-b)=m-n+a-b | ||
| C. | x-(3y-$\frac{1}{2}$)=x-3y+$\frac{1}{2}$ | D. | -$\frac{1}{2}$(4x-6y+3)=-2x+3y+3 |
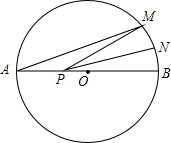 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5.
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为5. 如图,⊙O为△ABC的外接圆,弦CD平分△ABC的外角∠ACE.求证:OD⊥AB.
如图,⊙O为△ABC的外接圆,弦CD平分△ABC的外角∠ACE.求证:OD⊥AB.
 如图,AB是⊙O的直径,C是AB弧上一点,AP平分∠BAC,AB=3,AC=1,则PB=$\sqrt{3}$.
如图,AB是⊙O的直径,C是AB弧上一点,AP平分∠BAC,AB=3,AC=1,则PB=$\sqrt{3}$.