题目内容
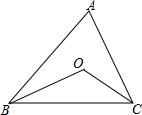 如图,在△ABC中,OB、OC分别平分∠ABC、∠ACB.
如图,在△ABC中,OB、OC分别平分∠ABC、∠ACB.(1)若∠ABC=50°,∠ACB=60°,则∠BOC=
(2)若∠A=70°,则∠BOC=
(3)若∠A=n°,则∠BOC=
考点:三角形内角和定理
专题:
分析:(1)根据角平分线的定义求出∠OBC、∠OCB,然后利用三角形的内角和等于180°列式计算即可得解;
(2)根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理列式计算即可得解;
(3)求解方法与(2)相同.
(2)根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理列式计算即可得解;
(3)求解方法与(2)相同.
解答:解:(1)∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC=
∠ABC=
×50°=25°,
∠OCB=
∠ACB=
×60°=30°,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-25°-30°=125°;
(2)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×110°=55°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°;
(3)∵∠A=n°,
∴∠ABC+∠ACB=180°-∠A=180°-n°,
∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×(180°-n°),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-
×(180°-n°)=90°+
n°,
所以,∠BOC=90°+
∠A.
故答案为:(1)125;(2)125;(3)90°+
n°,90°+
∠A.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-25°-30°=125°;
(2)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°;
(3)∵∠A=n°,
∴∠ABC+∠ACB=180°-∠A=180°-n°,
∵OB、OC分别平分∠ABC、∠ACB,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
所以,∠BOC=90°+
| 1 |
| 2 |
故答案为:(1)125;(2)125;(3)90°+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,熟记定理与概念并准确识图是解题的关键,难点在于整体思想的利用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
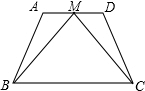 已知梯形ABCD中,AD∥BC,M是AD的中点,∠MBC=∠MCB,求证:梯形ABCD是等腰梯形.
已知梯形ABCD中,AD∥BC,M是AD的中点,∠MBC=∠MCB,求证:梯形ABCD是等腰梯形.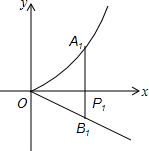 如图,分别过点Pi(i,0)(i=1、2、…、10)作x轴的垂线,交
如图,分别过点Pi(i,0)(i=1、2、…、10)作x轴的垂线,交 有理数a,b在数轴上(如图),那么
有理数a,b在数轴上(如图),那么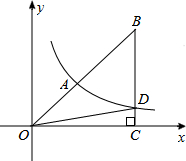 如图,双曲线y=
如图,双曲线y= 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.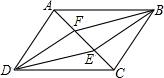 已知E,F是平行四边形ABCD对角线AC上的两个点,BF∥DE,连接DF,BE,则四边形BFDE是平行四边形吗?说明理由.
已知E,F是平行四边形ABCD对角线AC上的两个点,BF∥DE,连接DF,BE,则四边形BFDE是平行四边形吗?说明理由.