题目内容
等腰三角形的一个角是70°，求叧两个角．
考点：等腰三角形的性质
专题：分类讨论
分析：可分底角为70°和顶角为70°，再结合等腰三角形的性质和三角形内角和定理可求得另两个角．
解答：解：当底角为70°时，则另一个底角为70°，则顶角为180°-2×70°=40°，即另两个角分别为70°和40°；
当顶角为70°时，则另两个角为底角，大小为
=55°，即另两个角分别为55°和55°；
综上可知另两个角分别为70°、40°或55°、55°．
当顶角为70°时，则另两个角为底角，大小为
| 180°-70° |
| 2 |
综上可知另两个角分别为70°、40°或55°、55°．
点评：本题主要考查等腰三角形的性质，掌握等腰三角形的两底角相等是解题的关键，注意三角形内角和定理及分类讨论思想的应用．
练习册系列答案
相关题目
在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（ ）
A、 |
B、 |
C、 |
D、 |
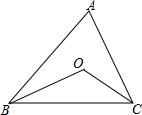如图，在△ABC中，OB、OC分别平分∠ABC、∠ACB．
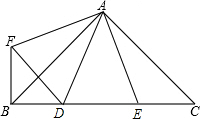如图，在Rt△ABC中，AB=AC，∠BAC=90°，D、E为BC上两点，∠DAE=45°，过点A作AF⊥AE，且AF=AE，连接BF、EF．
正比例函数y=kx和y=2kx（k是常数且k＞0）的图象如图，它们与反比例函数y=
如图，在?ABCD中，EF过对角线交点O，分别交AD，BC于点E，F，点G，H分别是OA与OC的中点，试判断四边形EGFH的形状，并证明你的结论．
已知线段m，n，用尺规作一条线段AB，使AB=m+n．
如图，在?ABCD中，点E，F在AD，BC上，且AE=CF，AF与BE交于点M，CE与DF交于点N，求证：四边形EMFN是平行四边形．
已知平行四边形中空白部分的面积是77平方厘米，求图中阴影部分的面积．