题目内容
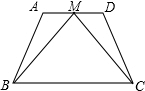 已知梯形ABCD中,AD∥BC,M是AD的中点,∠MBC=∠MCB,求证:梯形ABCD是等腰梯形.
已知梯形ABCD中,AD∥BC,M是AD的中点,∠MBC=∠MCB,求证:梯形ABCD是等腰梯形.考点:等腰梯形的判定
专题:证明题
分析:根据AD∥BC,得出∠MBC=∠AMB,∠MCB=∠DMC,再根据∠MBC=∠MCB,得出∠AMB=∠DMC,在△AMB和△DMC中,根据SAS得出△AMB≌△DMC,即可得出答案.
解答:证明:∵AD∥BC,
∴∠MBC=∠AMB,∠MCB=∠DMC,
∵∠MBC=∠MCB,
∴∠AMB=∠DMC,
在△AMB和△DMC中,
,
∴△AMB≌△DMC(SAS),
∴AB=DC,
∴ABCD是等腰梯形.
∴∠MBC=∠AMB,∠MCB=∠DMC,
∵∠MBC=∠MCB,
∴∠AMB=∠DMC,
在△AMB和△DMC中,
|
∴△AMB≌△DMC(SAS),
∴AB=DC,
∴ABCD是等腰梯形.
点评:此题考查了等腰梯形的判定和全等三角形的判定和性质,解答此题的关键是根据SAS证出△AMB≌△DMC.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
拒绝“餐桌浪费”刻不容缓,据统计,全国每年浪费食物总量约为50000000000kg,这个数据(保留2个有效数字)用科学记数法表示为( )
| A、0.5×1011 kg |
| B、50×109kg |
| C、5×1010kg |
| D、5.0×1010kg |
在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A、 |
B、 |
C、 |
D、 |
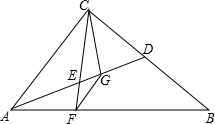 如图,△ABC中,∠ACB=90°,AD为BC边上的中线,点E为AD中点,CE的延长线交AB于点F,FG∥AC,交AD于点G,连接CG.求证:
如图,△ABC中,∠ACB=90°,AD为BC边上的中线,点E为AD中点,CE的延长线交AB于点F,FG∥AC,交AD于点G,连接CG.求证: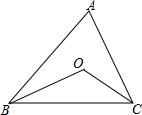 如图,在△ABC中,OB、OC分别平分∠ABC、∠ACB.
如图,在△ABC中,OB、OC分别平分∠ABC、∠ACB.