题目内容
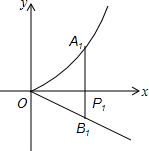 如图,分别过点Pi(i,0)(i=1、2、…、10)作x轴的垂线,交y=
如图,分别过点Pi(i,0)(i=1、2、…、10)作x轴的垂线,交y=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| A1B1 |
| 1 |
| A2B2 |
| 1 |
| A10B10 |
考点:二次函数图象上点的坐标特征,一次函数图象上点的坐标特征
专题:规律型
分析:根据Ai的纵坐标与Bi纵坐标的绝对值之和为AiBi的长,分别表示出所求式子的各项,拆项后抵消即可得到结果.
解答:解:∵分别过点Pi(i,0)(i=1、2、…、2014)作x轴的垂线,交y=
x2的图象于点Ai,交直线y=-
x于点Bi,
∴AiBi=
x2-(-
x)=
x(x+1),
∴
=
=2(
-
),
∴
+
+…+
=2(1-
+
-
+…+
-
)=
.
故答案为
.
| 1 |
| 2 |
| 1 |
| 2 |
∴AiBi=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| AiBi |
| 2 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |
∴
| 1 |
| A1B1 |
| 1 |
| A2B2 |
| 1 |
| A10B10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 10 |
| 1 |
| 11 |
| 20 |
| 11 |
故答案为
| 20 |
| 11 |
点评:此题考查了二次函数与一次函数图象上点的坐标特征,属于规律型试题,找出题中的规律是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
拒绝“餐桌浪费”刻不容缓,据统计,全国每年浪费食物总量约为50000000000kg,这个数据(保留2个有效数字)用科学记数法表示为( )
| A、0.5×1011 kg |
| B、50×109kg |
| C、5×1010kg |
| D、5.0×1010kg |
在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )
A、 |
B、 |
C、 |
D、 |
二次函数y=-
x2+
x+1000的图象经过第一象限的整格点(即纵、横坐标是正整数的点) 共有( )个.
| 1 |
| 2 |
| 1999 |
| 2 |
| A、1 000 |
| B、1 001 |
| C、1 999 |
| D、2 001 |
 如图,已知直线AB,CD,EF相交于点O,∠AOG=90°,∠FOG=32°,∠COE=38°,求∠BOD的度数.
如图,已知直线AB,CD,EF相交于点O,∠AOG=90°,∠FOG=32°,∠COE=38°,求∠BOD的度数.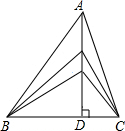 如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.
如图,△ABC边BC的长为10cm,BC边上的高为AD,当点A沿AD所在直线向点D运动时,三角形的面积发生了变化.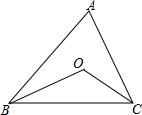 如图,在△ABC中,OB、OC分别平分∠ABC、∠ACB.
如图,在△ABC中,OB、OC分别平分∠ABC、∠ACB. 已知线段m,n,用尺规作一条线段AB,使AB=m+n.
已知线段m,n,用尺规作一条线段AB,使AB=m+n.