题目内容
13.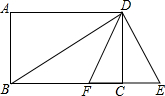 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+y2-8y的值为( )
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+y2-8y的值为( )| A. | 16 | B. | 15 | C. | 13 | D. | 0 |
分析 根据矩形的性质得到CD=AB=x,BC=AD=y,然后利用直角△BDE的斜边上的中线性质得出BF=DF=EF=4,则在直角△DCF中,利用勾股定理求得x2+(y-4)2=DF2,即可得出结果.
解答 解:∵四边形ABCD是矩形,AB=x,AD=y,
∴CD=AB=x,BC=AD=y,∠BCD=90°.
又∵BD⊥DE,点F是BE的中点,DF=4,
∴BF=DF=EF=4.
∴CF=BC-BF=y-4.
∴在直角△DCF中,DC2+CF2=DF2,即x2+(y-4)2=42=16,
∴x2+y2-8y+16=16,
∴x2+y2-8y=0.
故选:D.
点评 本题考查了勾股定理,直角三角形斜边上的中线以及矩形的性质.根据“直角△BDE的斜边上的中线等于斜边的一半”求得BF的长度是解题的突破口.

练习册系列答案
相关题目
2.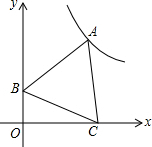 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )| A. | (3$\sqrt{3}$,4) | B. | (4,3$\sqrt{3}$) | C. | (4$\sqrt{3}$,3) | D. | (3,4$\sqrt{3}$) |
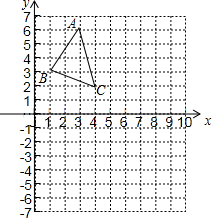 如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).
如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).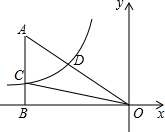 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.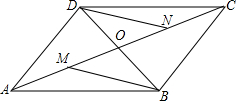 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论. 如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.
如图,在矩形ABCD中,对角线AC、BD相交于点O.求证:AC=BD.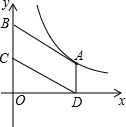 如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.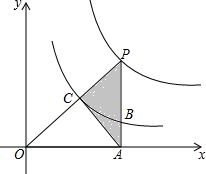 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )