题目内容
15.计算(1)6$\sqrt{2}$$+8\sqrt{2}$$-5\sqrt{2}$
(2)|$\sqrt{2}$-$\sqrt{3}$|$+2\sqrt{2}$.
分析 (1)直接合并同类二次根式求出答案;
(2)首先去绝对值,进而合并同类二次根式求出答案.
解答 解:(1)6$\sqrt{2}$$+8\sqrt{2}$$-5\sqrt{2}$=9$\sqrt{2}$;
(2)|$\sqrt{2}$-$\sqrt{3}$|$+2\sqrt{2}$
=$\sqrt{3}$-$\sqrt{2}$+2$\sqrt{2}$
=$\sqrt{3}$+$\sqrt{2}$.
点评 此题主要考查了二次根式的加减运算,正确掌握运算法则是解题关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
6.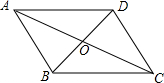 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )| A. | DC=BC | B. | AC⊥BD | C. | AB=BD | D. | ∠ADB=∠CDB |
3.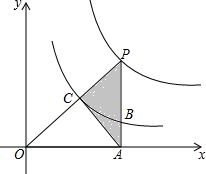 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
 如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )
如图所示,已知点P为反比例函数y=$\frac{4}{x}$(x>0)图象上的一点,且PA⊥x轴于点A,PA,PO分别交于反比例函数y=$\frac{1}{x}$图象于B,C两点,则△PAC的面积为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
10.若点(-2,y1),(-1,y2)(1,y3)在反比例函数y=$-\frac{2}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
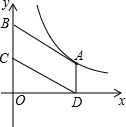 如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.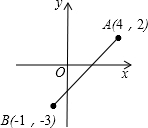 如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.