题目内容
10.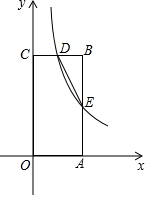 如图,在直角坐标系中,四边形OABC是矩形,点D(1,4)是BC中点,反比例函数y=$\frac{k}{x}$的图象经过点D,并交AB于点E.
如图,在直角坐标系中,四边形OABC是矩形,点D(1,4)是BC中点,反比例函数y=$\frac{k}{x}$的图象经过点D,并交AB于点E.(1)求k的值;
(2)求五边形OAEDC的面积S.
分析 (1)直接将D点坐标代入函数解析式得出答案;
(2)首先求出E点坐标,进而得出△BDE的面积,进而得出答案.
解答 解:(1)把D(1,4)代入y=$\frac{k}{x}$得,k=1×4=4;
(2)∵四边形OABC是矩形,
∴D(1,4)是BC中点,
∴BC=2CD=2,
∴B点坐标为:(2,4),
∵k=4,
∴y=$\frac{4}{x}$,
把x=2代入y=$\frac{4}{x}$得y=$\frac{4}{2}$=2,
∴E(2,2),
∴BE=2,
∴S△EBD=$\frac{1}{2}$×2×1=1,
∴S=2×4-1=7,
∴五边形OAEDC的面积为:7.
点评 此题主要考查了矩形的性质以及反比例函数系数k的几何意义,正确得出E点坐标是解题关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
20.计算(3a-2b)2的结果为( )
| A. | 9a2+4b2 | B. | 9a2+6ab+4b2 | C. | 9a2-12ab+4b2 | D. | 9a2-4b2 |
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.下列说法正确的是( )
| A. | 不可能事件发生的概率为1 | |
| B. | 随机事件发生的概率为$\frac{1}{3}$ | |
| C. | 概率很小的事件不可能发生 | |
| D. | 掷一枚质地均匀的硬币,正面朝上的概率为$\frac{1}{2}$ |
10.五一假期,小明和小华共同设计了一款拼图,他们用乒乓球粘成了下面几种造型的拼板(每种一块,没有重复):
(1)你能用部分拼板拼成图1中的平行四边形吗?所使用的拼板形状不能重复,请在图1中用不同颜色或底纹画出来.
(2)如图2,小华想用拼板摆出一个三棱锥造型,三棱锥的每条棱上有三个乒乓球,他已经用A5和B完成了一部分(图2是从上往下看的样子),请从剩下的拼板中挑出一块完成拼图,你认为需要的拼板是A1.
(3)小明试图用部分拼板拼出图3中的大三角形,请判断他能否成功?如果能,在图3中用不同颜色或底纹画出拼板的摆法;如果不能,请说明理由.
| A组 |  |  | 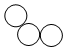 | |||
| A1 | A2 | A3 | ||||
| B组 | 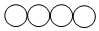 | 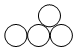 | 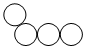 |  |  |  |
| B1 | B2 | B3 | B4 | B5 | B6 |
(2)如图2,小华想用拼板摆出一个三棱锥造型,三棱锥的每条棱上有三个乒乓球,他已经用A5和B完成了一部分(图2是从上往下看的样子),请从剩下的拼板中挑出一块完成拼图,你认为需要的拼板是A1.
(3)小明试图用部分拼板拼出图3中的大三角形,请判断他能否成功?如果能,在图3中用不同颜色或底纹画出拼板的摆法;如果不能,请说明理由.

 如图,若∠1=∠2=∠3=48°,则∠4=132°.
如图,若∠1=∠2=∠3=48°,则∠4=132°.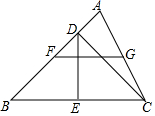 如图,CD是△ABC的高,E,F,G分别是BC,AB,AC上的中点,求证:FG=DE.
如图,CD是△ABC的高,E,F,G分别是BC,AB,AC上的中点,求证:FG=DE.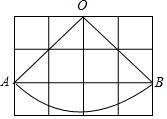 如图,已知小正方形方格的边长为1cm,点O,A,B分别是格点,以O为圆心,OA长为半径作扇形OAB,则弧AB的长为$\sqrt{2}$πcm(结果保留π和根号)
如图,已知小正方形方格的边长为1cm,点O,A,B分别是格点,以O为圆心,OA长为半径作扇形OAB,则弧AB的长为$\sqrt{2}$πcm(结果保留π和根号)