题目内容
18.下列说法正确的是( )| A. | 不可能事件发生的概率为1 | |
| B. | 随机事件发生的概率为$\frac{1}{3}$ | |
| C. | 概率很小的事件不可能发生 | |
| D. | 掷一枚质地均匀的硬币,正面朝上的概率为$\frac{1}{2}$ |
分析 不可能发生的事件就是一定不会发生的事件,因而概率为0.
不确定事件就是随机事件,即可能发生也可能不发生的事件,发生的概率>0并且<1.
解答 解:A、不可能事件发生的概率为0,故错误;
B、随机事件发生的概率介于0和1之间,不一定是$\frac{1}{3}$,故错误;
C、概率很小的事件不是不可能发生,而是发生的机会较小,故错误;
D、抛一枚质地均匀的硬币,正面朝上和反面朝上的可能性相等,都是$\frac{1}{2}$,故正确.
故选D.
点评 本题考查了概率的意义:一般地,在大量重复实验中,如果事件A发生的频率mn会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记为P(A)=p;概率是频率(多个)的波动稳定值,是对事件发生可能性大小的量的表现.必然发生的事件的概率P(A)=1;不可能发生事件的概率P(A)=0.

练习册系列答案
相关题目
8.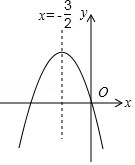 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
9.如果向东走3米记作+3 米,那么向西走2 米记作( )
| A. | $\frac{1}{2}$米 | B. | $-\frac{1}{2}$米 | C. | 2 米 | D. | -2 米 |
6.-8的绝对值是( )
| A. | -8 | B. | 8 | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
15.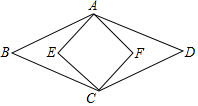 如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
 如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{3}$:1 | C. | 2:1 | D. | 2:$\sqrt{3}$ |
16. 如图,A,B,C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )
如图,A,B,C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )

 如图,A,B,C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )
如图,A,B,C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是( )
| A. | A | B. | B | C. | C | D. | D |
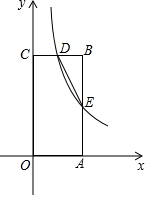 如图,在直角坐标系中,四边形OABC是矩形,点D(1,4)是BC中点,反比例函数y=$\frac{k}{x}$的图象经过点D,并交AB于点E.
如图,在直角坐标系中,四边形OABC是矩形,点D(1,4)是BC中点,反比例函数y=$\frac{k}{x}$的图象经过点D,并交AB于点E.