题目内容
3.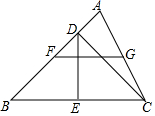 如图,CD是△ABC的高,E,F,G分别是BC,AB,AC上的中点,求证:FG=DE.
如图,CD是△ABC的高,E,F,G分别是BC,AB,AC上的中点,求证:FG=DE.
分析 根据直角三角形的性质得到DE=$\frac{1}{2}$BC,根据三角形中位线定理得到FG=$\frac{1}{2}$BC,证明结论.
解答 证明:∵CD是△ABC的高,
∴∠BDC=90°,
∵E是AC的中点,
∴DE=$\frac{1}{2}$BC,
∵F,G分别是AB,AC上的中点,
∴FG=$\frac{1}{2}$BC,
∴FG=DE.
点评 本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
5.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | ${(\frac{1}{2})}^{-1}$=2 | D. | ${(\frac{1}{2})}^{0}$=0 |
6.-8的绝对值是( )
| A. | -8 | B. | 8 | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
15.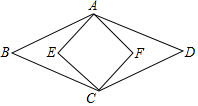 如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
 如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )
如图,菱形ABCD和正方形AECF,菱形的一个锐角为60度,则菱形ABCD和正方形AECF面积比为( )| A. | $\sqrt{3}$:$\sqrt{2}$ | B. | $\sqrt{3}$:1 | C. | 2:1 | D. | 2:$\sqrt{3}$ |
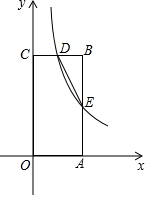 如图,在直角坐标系中,四边形OABC是矩形,点D(1,4)是BC中点,反比例函数y=$\frac{k}{x}$的图象经过点D,并交AB于点E.
如图,在直角坐标系中,四边形OABC是矩形,点D(1,4)是BC中点,反比例函数y=$\frac{k}{x}$的图象经过点D,并交AB于点E.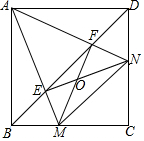 如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.
如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.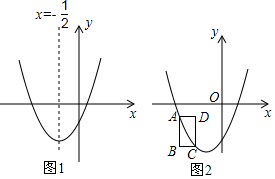
 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: