题目内容
8.既是方程x+3y=5的解,又是方程x-3y=-1的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.分析 两个方程组成方程组,求出方程组的解即可.
解答 解:解方程组$\left\{\begin{array}{l}{x+3y=5}\\{x-3y=-1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 本题考查了二元一次方程的解和解二元一次方程组,能求出方程组的解是解此题的关键.

练习册系列答案
相关题目
16.将(mx+3)(2-3x)展开后,结果不含x的一次项,则m的值为( )
| A. | 0 | B. | $\frac{9}{2}$ | C. | -$\frac{9}{2}$ | D. | $\frac{3}{2}$ |
3.15:40时,时针与分针所成角的度数是( )
| A. | 120 | B. | 130 | C. | 140 | D. | 150 |
20.在对-$\frac{3}{4}$a2x+3axy2进行因式分解时,公因式最好是( )
| A. | ax | B. | $\frac{3}{4}$ax | C. | -$\frac{3}{4}$ax | D. | -$\frac{1}{4}$ax |
18.(1)问题背景
如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

请直接写出四边形ABCD的面积为25.
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 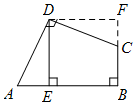 |
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
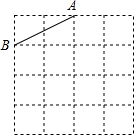 已知格点△ABC的一边AB如图,方格中小正方形的边长为1,若另一边AC=$\sqrt{10}$,在如图中画出△ABC(只需画出满足的一个)并回答如下问题:
已知格点△ABC的一边AB如图,方格中小正方形的边长为1,若另一边AC=$\sqrt{10}$,在如图中画出△ABC(只需画出满足的一个)并回答如下问题: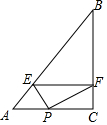 如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.
如图,△ABC中,∠C=90°,BC=4,AC=3,P是边AC上的一动点,PE⊥AB于点E,EF⊥BC于点F.设AP=x,则能使以点P、C、F为顶点的三角形与以A、P、E为顶点的三角形相似的x=$\frac{75}{34}$或$\frac{75}{41}$.