题目内容
已知Rt△ABC中,∠C=90°,AC=6,BC=8,点O和M分别为Rt△ABC的外心和内心,线段OM的长为 .
考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.先根据勾股定理求出AB=10,得到△ABC的外接圆半径AO=5,再证明四边形MECD是正方形,根据内心的性质和切线长定理,求出⊙M的半径r=2,则ON=1,然后在Rt△OMN中,运用勾股定理即可求解.
解答: 解:如图,作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.
解:如图,作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.
在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB=
=10.
∵点O为△ABC的外心,
∴AO为外接圆半径,AO=
AB=5.
设⊙M的半径为r,则MD=ME=r,
又∵∠MDC=∠MEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∵AB=10,
∴8-r+6-r=10,
解得r=2,
∴MN=r=2,AN=6-r=4.
在Rt△OIN中,∵∠MNO=90°,ON=AO-AN=5-4=1,
∴OM=
=
.
故答案是:
.
 解:如图,作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.
解:如图,作△ABC的内切圆⊙M,过点M作MD⊥BC于D,ME⊥AC于E,MN⊥AB于N.在Rt△ABC中,∵∠ACB=90°,AC=6,BC=8,
∴AB=
| AC2+BC2 |
∵点O为△ABC的外心,
∴AO为外接圆半径,AO=
| 1 |
| 2 |
设⊙M的半径为r,则MD=ME=r,
又∵∠MDC=∠MEC=∠C=90°,
∴四边形IECD是正方形,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∵AB=10,
∴8-r+6-r=10,
解得r=2,
∴MN=r=2,AN=6-r=4.
在Rt△OIN中,∵∠MNO=90°,ON=AO-AN=5-4=1,
∴OM=
| MN2+ON2 |
| 5 |
故答案是:
| 5 |
点评:此题考查了直角三角形的外心与内心的概念及性质,勾股定理,正方形的判定与性质,切线长定理,综合性较强,难度适中.求出△ABC的内切圆半径是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
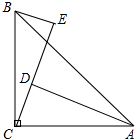 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.| A、0.7 | B、1.7 |
| C、3.3 | D、2.3 |
已知在⊙O中,半径r=13,弦AB∥CD,且AB=24,CD=10,则AB与CD的距离为( )
| A、5 | B、7 | C、17 | D、7或17 |
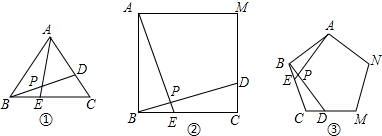
 如图为正方形空地的绿化带设计方案,阴影部分为绿化带,根据题中给出的数据,分别就两种方案表示出绿化带的面积.
如图为正方形空地的绿化带设计方案,阴影部分为绿化带,根据题中给出的数据,分别就两种方案表示出绿化带的面积.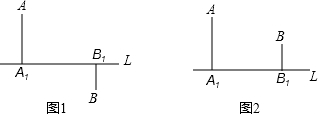
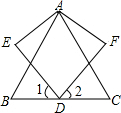 如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.
如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.