题目内容
11．解方程组：$\left\{\begin{array}{l}{x+y=5}\\{x-2y=-10}\end{array}\right.$．分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{x+y=5①}\\{x-2y=-10②}\end{array}\right.$，
①-②得：3y=15，即y=5，
把y=5代入①得：x=0，
则方程组的解为$\left\{\begin{array}{l}{x=0}\\{y=5}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在平面直角坐标系上有点A（1，0），点A第一次跳动至点A1（-1，1），第四次向右跳动5个单位支至点A4（3，2），依此规律跳动下去，点A第2016次跳动至点A2016的坐标是（1009，1008）．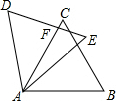
如图，将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED，边AC与DE交于点F，则AF的长为3$\sqrt{3}$．
如图，△ABC是等腰直角三角形，AC=4，直线l垂直平分AC交AC于点D，点P在直线l上，求△APB的周长的最小值4+4$\sqrt{2}$．
20．已知，在平面直角坐标系xOy中，点A（-4，0 ），点B在直线y=x+2上．当A，B两点间的距离最小时，点B的坐标是（ ）
| A． | （$-2-\sqrt{2}$，$-\sqrt{2}$） | B． | （$-2-\sqrt{2}$，$\sqrt{2}$） | C． | （-3，-1 ） | D． | （-3，$-\sqrt{2}$） |
