题目内容
7.将线段AB延长至C,使BC=$\frac{1}{3}$AB,延长BC至点D,使CD=$\frac{1}{3}$BC,延长CD至点E,使DE=$\frac{1}{3}$CD,若CE=8cm.(1)求AB的长度;
(2)如果点M是线段AB中点,点N是线段AE中点,求MN的长度.
分析 (1)根据CE的长,可得关于x的方程,根据BC=$\frac{1}{3}$AB,延长BC至点D,使CD=$\frac{1}{3}$BC,延长CD至点E,使DE=$\frac{1}{3}$CD,可得AB的长;
(2)根据线段的和差,可得AE的长,根据线段中点的性质,可得AN,AM的长,根据线段的和差,可得答案.
解答 解:如图: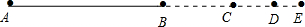 ,
,
设DE=x,由BC=$\frac{1}{3}$AB,延长BC至点D,使CD=$\frac{1}{3}$BC,延长CD至点E,使DE=$\frac{1}{3}$CD,得
CD=3x,BC=9x,AB=27x.
由线段的和差,得
CE=BC+DE=4x,DE=8,
解得x=2,
AB=27x=54;
(2)由线段的和差,得
AE=AB+BC+CD+DE=27x+9x+3x+x=40x=80,
由点M是线段AB中点,点N是线段AE中点,得
AM=$\frac{1}{2}$AB=$\frac{1}{2}$×54=27,AN=$\frac{1}{2}$AE=$\frac{1}{2}$×80=40,
由线段的和差,得
MN=AN-AM=40-27=13.
点评 本题考查了两点间的距离,利用线段的和差得出关于x的方程是解题关键,又利用了线段中点的性质.

练习册系列答案
相关题目
6.甲、乙两名运动员在六次射击测试中的成绩如下表(单位:环):
如果两人测试成绩的中位数相同,那么乙第四次射击的成绩(表中标记为“?”)可以是( )
| 甲的成绩 | 6 | 7 | 8 | 8 | 9 | 9 |
| 乙的成绩 | 5 | 9 | 6 | ? | 9 | 10 |
| A. | 6环 | B. | 7环 | C. | 8环 | D. | 9环 |
12.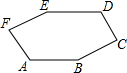 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
 如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )
如图,已知AB∥ED,∠C=90°,∠ABC=∠DEF,∠D=130°,∠F=100°,则∠E的度数为( )| A. | 160° | B. | 150° | C. | 145° | D. | 140° |
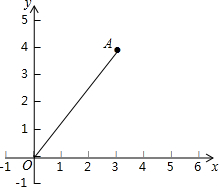 在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.
在直角坐标系中,O为坐标原点,已知A(3,4),在x轴上确定一点P,使△OAP为等腰三角形,求符合条件的点P的坐标.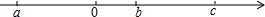 实数a,b,c在数轴上的位置如图所示.
实数a,b,c在数轴上的位置如图所示.