题目内容
10.(1)如图1,OP是∠MON的平分线,请利用该图形,借助直尺和圆规画一组已OP所在直线为对称轴且一条边在OP上的全等三角形,并用符号表示出来;(不写作法,保留作图痕迹,不要证明)(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图2:在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试证明:BC=AC+AD;
②如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

分析 (1)在OP上任意取一点A,在OM、ON上分别截取OC,OB,使得OC=OB,则有,△AOB≌△AOC;
(2)如图2,截取CE=CA,连接DE,只要证明△CAD≌△CED,DE=EB即可解决问题;、
(3)截取AE=AD,连接CE,作CH⊥AB,垂足为点H,设EH=HB=x,首先证明△ADC≌△AEC,在Rt△ACH和Rt△CEH中利用勾股定理可得172-(9+x)2=102-x2,求出x即可解决问题.
解答 (1)解:如图1,△AOB≌△AOC.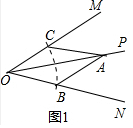
(2)证明:如图2,截取CE=CA,连接DE,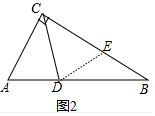
∵CD平分∠ACB,
∴∠ACD=∠ECD,
在△ACD与△ECD中,
∵$\left\{\begin{array}{l}{AC=CE}\\{∠ACD=∠ECD}\\{CD=CD}\end{array}\right.$,
∴△CAD≌△CED,
∴AD=DE,∠A=∠CED=60°,AC=CE,
∵∠ACB=90°,∠A=60°,
∴∠B=30°,
∴∠B=∠EDB=30°,
∴DE=EB=AD,
∴BC=AC+AD;
(3)解:截取AE=AD,连接CE,作CH⊥AB,垂足为点H,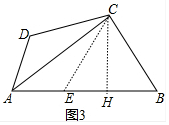
同理△ADC≌△AEC,
∴AE=AD=9,CD=CE=10=CB,
∵CH⊥AB,CE=CB,
∴EH=HB,
设EH=HB=x,在Rt△ACH和Rt△CEH中
172-(9+x)2=102-x2,
解得:x=6,
∴AB=21.
点评 本题考查三角形综合题、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.以下命题为真命题的是( )
| A. | 相等的角是对顶角 | B. | 两直线平行,同旁内角互补 | ||
| C. | 若a2=b2,则a=b | D. | 若a2+b2>0,则a>0,b>0 |
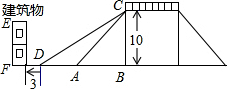 如图是一座人行天桥示意图:天桥的高是10米,坡面的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的坡度为$\sqrt{3}$:3,若新坡角下需留3米的人行道,问离原坡面点A处10米的建筑物EF是否需要拆除?($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图是一座人行天桥示意图:天桥的高是10米,坡面的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的坡度为$\sqrt{3}$:3,若新坡角下需留3米的人行道,问离原坡面点A处10米的建筑物EF是否需要拆除?($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)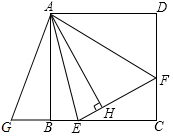 如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为6.
如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为6.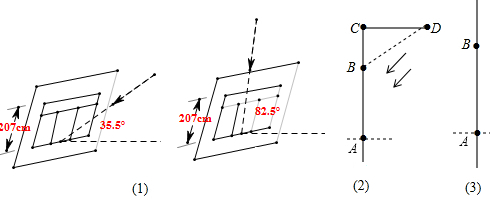
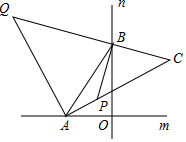 如图,直线m与直线n互相垂直,垂足为O,A、B两点同时从点O出发,点A沿直线m向左运动,点B沿直线n向上运动.
如图,直线m与直线n互相垂直,垂足为O,A、B两点同时从点O出发,点A沿直线m向左运动,点B沿直线n向上运动.