Question

1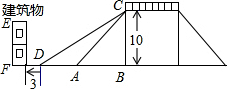．如图是一座人行天桥示意图：天桥的高是10米，坡面的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面的坡度为$\sqrt{3}$：3，若新坡角下需留3米的人行道，问离原坡面点A处10米的建筑物EF是否需要拆除？（$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

Answer 1

分析 直接利用等腰直角三角形的性质得出AB的长，再利用锐角三角函数关系得出DB的长，进而得出答案．

解答 解：∵∠CAB=45°，
∴AB=BC=10，
∵∠CDB=30°，
∴BD=$\frac{10}{tan30°}$=10$\sqrt{3}$（m），
∴AD=10$\sqrt{3}$-10≈7.32（m），
∵7.32+3＞10，
答：离原坡角10米的建筑物需要拆除．

点评 此题主要考查了解直角三角形的应用，正确得出BD的长是解题关键．