题目内容
6.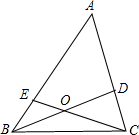 如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )
如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 连接AO,利用等高不等底的三角形面积比等于底长的比,可求出△COD与△BOE的面积.列出关于△AOE与△AOD的面积的方程即可求出四边形AEOD的面积.
解答 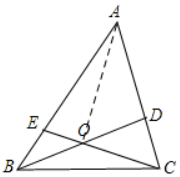 解:连接OA,
解:连接OA,
∵OB=OD,
∴S△BOC=S△COD=2,
∵OC=2OE,
∴S△BOE=$\frac{1}{2}$S△BOC=1,
∵OB=OD,
∴S△AOB=S△AOD,
∴S△BOE+S△AOE=S△AOD,
即:1+S△AOE=S△AOD①,
∵OC=2OE,
∴S△AOC=2S△AOE,
∴S△AOD+S△COD=2S△AOE,
即:S△AOD+2=2S△AOE②,
联立①和②:解得:S△AOE=3,S△AOD=4,
S四边形AEOD=S△AOE+S△AOD=7,
故选(D)
点评 本题考查三角形面积问题,涉及方程组的解法,注意灵活运用等高不等底的三角形面积比等于底长的比这一结论.

练习册系列答案
相关题目
11.据报道,目前我国“神威﹒太湖之光”超级计算机的运算速度位居全球第一,其运算速度达到了每秒1250000000亿次,数字1250000000用科学记数法可简洁表示为( )
| A. | 1.25×109 | B. | 0.125×1010 | C. | 12.5×108 | D. | 1.25×1010 |
9.函数y=kx2+mx+n是二次函数,则( )
| A. | k=0,m≠0,n≠0 | B. | k≠0,m≠0,n=0 | C. | k≠0 | D. | 以上都不正确 |
11.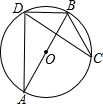 如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
 如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
15.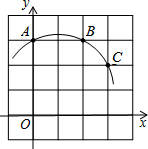 如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )
如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )
 如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )
如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )| A. | (0,0) | B. | (1,1) | C. | (0,1) | D. | (1,0) |
 如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=90°.
如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=90°.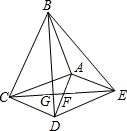 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论中,正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论中,正确的结论有( )