题目内容
1.已知a1=2,a2=2+4,a3=2+4+6,…,an=2+4+6+…+2n,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{99}}$+$\frac{1}{{a}_{100}}$=$\frac{100}{101}$.分析 先求出an=n(n+1)即可得到$\frac{1}{{a}_{n}}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$即可化简原式即可.
解答 解:由题意得,an=n(n+1)
∴$\frac{1}{{a}_{n}}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$
∴原式=$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-…+$\frac{1}{100}$-$\frac{1}{101}$=1-$\frac{1}{101}$=$\frac{100}{101}$,
故答案为:$\frac{100}{101}$.
点评 此题是规律型:数字的变化类,主要考查了偶数的和,解本题的关键是an=n(n+1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 按照图中的方法作图,作出的是( )
按照图中的方法作图,作出的是( )
 按照图中的方法作图,作出的是( )
按照图中的方法作图,作出的是( )| A. | 一个角等于已知角 | B. | 一条线段等于已知线段 | ||
| C. | 线段的垂直平分线 | D. | 角的平分线 |
11.下列式子中能用公式法分解因式的是( )
| A. | a2+ab+b2 | B. | a2+2a+2 | C. | a2-2b+b2 | D. | a2+2a+1 |
13.某商品价格a元,降低15%后又降价10%,销售额猛增,商店决定再提价20%,提价后这种产品价格为( )
| A. | a元 | B. | 0.918a元 | C. | 0.972a元 | D. | 0.96a元 |
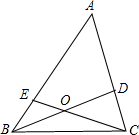 如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )
如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )