题目内容
15.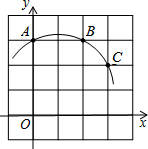 如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )
如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )| A. | (0,0) | B. | (1,1) | C. | (0,1) | D. | (1,0) |
分析 根据图形作线段AB和BC的垂直平分线,两线的交点即为圆心,根据图形得出即可.
解答  解:如图线段AB的垂直平分线即x=1,和线段CD的垂直平分线的交点即为弧的圆心.
解:如图线段AB的垂直平分线即x=1,和线段CD的垂直平分线的交点即为弧的圆心.
即圆心的坐标是(1,1),
故选B.
点评 本题考查了垂径定理,线段垂直平分线性质,坐标与图形性质的应用,数形结合是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
10.在一次游戏晚会上,老师出了一道题让小明猜一个自然数,题目如下:甲:这个数是9;乙:这个数是质数;丙:这个数是偶数;丁:这个数是15.若甲和乙之中有一个对,丙和丁之中有一个对,则这个数是( )
| A. | 3 | B. | 5 | C. | 2 | D. | 6 |
20.某工厂现有工人x人,若现有人数比去年原有人数减少25%,则该工厂原有人数为( )
| A. | $\frac{x}{1+25%}$ | B. | $\frac{x}{1-25%}$ | C. | (1+25%)x | D. | (1-25%)x |
7.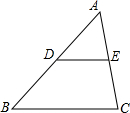 如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
 如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )| A. | BC=2DE | B. | △ADE∽△ABC | C. | $\frac{AD}{AE}$=$\frac{AB}{AC}$ | D. | S△ABC=2S△ADE |
5.下列计算正确的是( )
| A. | $\frac{1}{a}+\frac{1}{a}=\frac{1}{2a}$ | B. | $\frac{1}{a-b}+\frac{1}{b-a}=0$ | ||
| C. | $\frac{m-n}{a}-\frac{m+n}{a}=0$ | D. | $\frac{1}{{{{(a-b)}^2}}}+\frac{1}{{{{(b-a)}^2}}}=\frac{1}{{{{(a-b)}^2}}}$ |
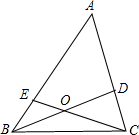 如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )
如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )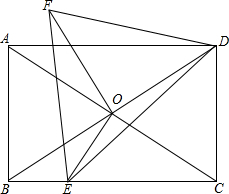 如图,矩形ABCD的对角线AC、BD交于点O,过点O作OE⊥AC,交BC于点E,将线段OD绕点O逆时针旋转90°得OF,连结FD,FE,DE,已知AB=6,BC=8,则S△EFD=$\frac{149}{8}$.
如图,矩形ABCD的对角线AC、BD交于点O,过点O作OE⊥AC,交BC于点E,将线段OD绕点O逆时针旋转90°得OF,连结FD,FE,DE,已知AB=6,BC=8,则S△EFD=$\frac{149}{8}$.