题目内容
13.先化简,再求值:①(x+1-$\frac{15}{x-1}$)÷$\frac{{x}^{2}-8x+16}{1-x}$,其中x=2;
②$(1+\frac{2}{p-2})$÷$\frac{{p}^{2}-p}{{p}^{2}-4}$,(其中p是满足-3<p<3的整数).
分析 (1)先括号内通分,然后计算除法,最后约分化简即可.
(2)先括号内通分,然后计算除法,最后约分化简,p=-1代入即可.
解答 解:(1)原式=$\frac{{x}^{2}-1-15}{x-1}$•$\frac{1-x}{(x-4)^{2}}$=$\frac{(x+4)(x-4)}{x-1}$•$\frac{1-x}{(x-4)^{2}}$=-$\frac{x+4}{x-4}$.
当x=2时,原式=-$\frac{2+4}{2-4}$=3.
(2)原式=$\frac{p-2+2}{p-2}$•$\frac{(p+2)(p-2)}{p(P-1)}$=$\frac{P+2}{P-1}$,
由题意p=-1,所以原式=$\frac{-1+2}{-1-1}$=-$\frac{1}{2}$.
点评 本题考查分式的化简求值.熟练掌握分式的混合运算法则是解题的关键,注意运算顺序,字母取值时应该注意使得代数式有意义,属于中考常考题型.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
4.下列各组数中,属于勾股数的是( )
| A. | 2.5,6,6.5 | B. | 5,7,10 | C. | $\sqrt{2},\sqrt{3},\sqrt{5}$ | D. | 6,8,10 |
1.下列各组中的两个“F”,通过平移可以重合在一起的是( )
| A. |  | B. |  | C. |  | D. |  |
5.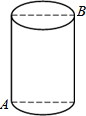 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
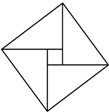 如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )
如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )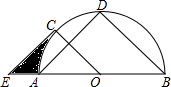 如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.
如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.