题目内容
8.计算:(1)(2a-3b)2(2a+3b)2;
(2)x2•x3+x7•x2
(3)(a2bc)2÷(ab2c)
(4)(2x+5y)(2x-5y)(-4x2-25y2).
分析 (1)根据平方差公式和完全平方公式进行计算即可;
(2)根据同底数幂的乘法以及合并同类项得法则进行计算即可;
(3)根据积的乘方、同底数幂的乘法和幂的乘方进行计算即可;
(4)根据平方差公式和完全平方公式进行计算即可.
解答 解:(1)原式=[(2a-3b)(2a+3b)]2
=(4a2-9b2)2
=16a4-72a2b2+81b4;
(2)原式=x3+2+x7+2
=x5+x9;
(3)原式=a4b2c2÷ab2c
=a3c;
(4)原式=-(4x2-25y2)(4x2+25y2)
=-[(4x2)2-(25y2)2]
=625y4-16x4.
点评 本题考查了整式的混合运算,熟记平方差公式和完全平方公式是解题的关

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
16.若a,b,c三个数满足a2+b2+c2=ab+bc+ac,则( )
| A. | a=b=c | B. | a,b,c不全相等 | ||
| C. | a,b,c互不相等 | D. | 无法确定a,b,c之间关系 |
3.使不等式x>-$\frac{7}{3}$且x<2同时成立的所有整数的和是( )
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
20.若等式$\sqrt{(x-2)(x+1)}$=$\sqrt{x-2}$$•\sqrt{x+1}$成立,则x的取值范围是( )
| A. | x≥2 | B. | x≥1 | C. | -1≤x≤2 | D. | x≤-1或x≥2 |
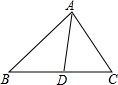 如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.
如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.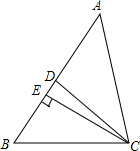 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.