题目内容
2.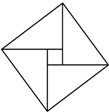 如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )
如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 根据勾股定理可以求得a2+b2等于大正方形的面积,然后求四个直角三角形的面积,即可得到ab的值.
解答 解:根据勾股定理可得a2+b2=17,
四个直角三角形的面积是:$\frac{1}{2}$ab×4=17-5=12,
即:ab=6.
故选:B.
点评 本题考查了勾股定理和正方形的性质,正确根据图形的关系求得a2+b2和ab的值是关键.

练习册系列答案
相关题目
10.某学习小组对20名男生60秒跳绳的成绩进行统计,其结果如下表所示:这20个数据的平均数和众数分别是( )
| 跳绳的成绩(个) | 130 | 135 | 140 | 145 | 150 |
| 人数(人) | 1 | 3 | 11 | 3 | 2 |
| A. | 140,3 | B. | 140.5,140 | C. | 140,135 | D. | 46.83,140 |
12. 如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
 如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )| A. | $\frac{DE}{AB}$=$\frac{DF}{BF}$ | B. | $\frac{AF}{FE}$=$\frac{BF}{FD}$ | C. | $\frac{AF}{AE}$=$\frac{DF}{BD}$ | D. | $\frac{DE}{DC}$=$\frac{EF}{AF}$ |
 如图,已知直线a∥b,c⊥d,∠1=36°,则∠2的度数是126°.
如图,已知直线a∥b,c⊥d,∠1=36°,则∠2的度数是126°.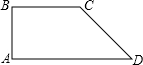 已知直角梯形上底3cm,下底5cm,另一个底角为45°,建立适当直角坐标系并写出图形中的四个顶点的坐标,求出梯形的面积.
已知直角梯形上底3cm,下底5cm,另一个底角为45°,建立适当直角坐标系并写出图形中的四个顶点的坐标,求出梯形的面积.