题目内容
5.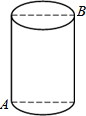 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
分析 此题最直接的解法就是将圆柱展开,然后利用两点之间线段最短解答.
解答  解:底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为:$\frac{1}{2}$×2π×$\frac{6}{π}$=6(cm),展开得:
解:底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为:$\frac{1}{2}$×2π×$\frac{6}{π}$=6(cm),展开得:
∵BC=8cm,AC=6cm,
根据勾股定理得:AB=$\sqrt{{8}^{2}+{6}^{2}}$=10(cm).
故选B.
点评 此题考查的是平面展开-最短路径问题,解题的关键是根据题意画出展开图,表示出各线段的长度,再利用勾股定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.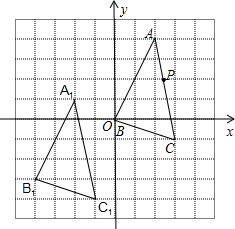 在如图的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P($\frac{12}{5}$,2)平移后的对应点P1,则点P1的坐标为( )
在如图的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P($\frac{12}{5}$,2)平移后的对应点P1,则点P1的坐标为( )
 在如图的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P($\frac{12}{5}$,2)平移后的对应点P1,则点P1的坐标为( )
在如图的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P($\frac{12}{5}$,2)平移后的对应点P1,则点P1的坐标为( )| A. | (-$\frac{7}{5}$,-1) | B. | (-$\frac{3}{2}$,-2) | C. | (-$\frac{8}{5}$,-1) | D. | (-$\frac{12}{5}$,-1) |
16.若a,b,c三个数满足a2+b2+c2=ab+bc+ac,则( )
| A. | a=b=c | B. | a,b,c不全相等 | ||
| C. | a,b,c互不相等 | D. | 无法确定a,b,c之间关系 |
20.若等式$\sqrt{(x-2)(x+1)}$=$\sqrt{x-2}$$•\sqrt{x+1}$成立,则x的取值范围是( )
| A. | x≥2 | B. | x≥1 | C. | -1≤x≤2 | D. | x≤-1或x≥2 |
10.某学习小组对20名男生60秒跳绳的成绩进行统计,其结果如下表所示:这20个数据的平均数和众数分别是( )
| 跳绳的成绩(个) | 130 | 135 | 140 | 145 | 150 |
| 人数(人) | 1 | 3 | 11 | 3 | 2 |
| A. | 140,3 | B. | 140.5,140 | C. | 140,135 | D. | 46.83,140 |
15.一艘轮船只有在涨潮的时候才能驶入港口,已知该港口每天涨潮的时间为早:5:00至7:00和下午5:00至6:00,则该船在一昼夜内可以进港的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{20}$ | D. | $\frac{1}{12}$ |