题目内容
3.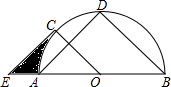 如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.
如图所示,AB为半圆O的直径,点D是半圆弧的中点,半径OC∥BD,过点C作AD的平行线交BA延长线于点E.(1)判断CE与半圆OD的位置关系,并证明你的结论.
(2)若BD=4,求阴影部分面积.
分析 (1)直接利用圆周角定理结合平行线的性质得出CO⊥EC,即可得出答案;
(2)利用已知得出△ADB为等腰直角三角形,进而得出△ECO为等腰直角三角形,由S阴影部分=S△ECD-S扇形AOC求出答案.
解答 解:(1)CE与半圆OD相切,
理由:∵AB为直径,
∴∠ADB=90°,
∴AD⊥DB,
∵CO∥DB,
∴CO⊥AD,
∵EC∥AD,
∴CO⊥EC,
∴CE与半圆OD相切;
(2)∵点D平分半圆弧,
∴∠B=45°,
∴△ADB为等腰直角三角形,
∵BD=4,
∴AB=4$\sqrt{2}$,
∴CO=2$\sqrt{2}$,
∵CO∥DB,
∴∠AOC=∠ABD=45°,
由(1)知CO⊥EC,
∴△ECO为等腰直角三角形,
∴S阴影部分=S△ECD-S扇形AOC=$\frac{1}{2}$(2$\sqrt{2}$)2-$\frac{45}{360}$π(2$\sqrt{2}$)2=4-π.
点评 此题主要考查了切线的判定以及等腰直角三角形的性质、扇形面积求法等知识,正确得出△ECO为等腰直角三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 矩形对角线垂直 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 等腰三角形两腰上的高相等 |
15.一艘轮船只有在涨潮的时候才能驶入港口,已知该港口每天涨潮的时间为早:5:00至7:00和下午5:00至6:00,则该船在一昼夜内可以进港的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{20}$ | D. | $\frac{1}{12}$ |
12. 如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
 如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在CD上,连接AE交BD于点F,则下列结论错误的是( )| A. | $\frac{DE}{AB}$=$\frac{DF}{BF}$ | B. | $\frac{AF}{FE}$=$\frac{BF}{FD}$ | C. | $\frac{AF}{AE}$=$\frac{DF}{BD}$ | D. | $\frac{DE}{DC}$=$\frac{EF}{AF}$ |
13.方程3x2-2$\sqrt{6}$x+2=0的根的情况是( )
| A. | 无实根 | B. | 有两个等根 | C. | 有两个不等根 | D. | 有分数根 |