题目内容
2.计算(1)$\sqrt{72}$-4$\sqrt{\frac{1}{2}}$-$\frac{1}{7}$$\sqrt{98}$+$\sqrt{1\frac{1}{8}}$;
(2)(7+4$\sqrt{3}$)(7-4$\sqrt{3}$)-(3$\sqrt{5}$-1)2;
(3)若最简二次根式$\root{a+1}{2a+5}$与$\sqrt{4a+3b}$是同类二次根式,求a、b的值.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式和完全平方公式计算;
(3)根据最简二次根式和同类二次根式的定义得到$\left\{\begin{array}{l}{a+1=2}\\{2a+5=4a+3b}\end{array}\right.$,然后解方程组即可.
解答 解:(1)原式=6$\sqrt{2}$-2$\sqrt{2}$-$\sqrt{2}$+$\frac{3\sqrt{2}}{4}$
=$\frac{15\sqrt{2}}{4}$;
(2)原式=49-48-(45-6$\sqrt{5}$+1)
=1-46+6$\sqrt{5}$
=-45+6$\sqrt{5}$;
(3)根据题意得$\left\{\begin{array}{l}{a+1=2}\\{2a+5=4a+3b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了同类二次根式的定义.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
17.无理数$\sqrt{12}-\sqrt{3}$的大小在以下两个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
14.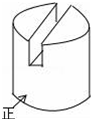 如图中几何体的左视图是( )
如图中几何体的左视图是( )
 如图中几何体的左视图是( )
如图中几何体的左视图是( )| A. | 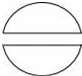 | B. |  | C. |  | D. | 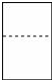 |
12.下列说法正确的个数有( )
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
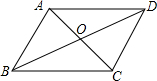 已知?ABCD,AC与BD相交于点O.
已知?ABCD,AC与BD相交于点O.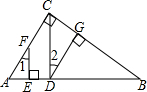 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试判断CD与AB的位置关系,并说明理由.请完成下列解答:
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试判断CD与AB的位置关系,并说明理由.请完成下列解答: