题目内容
6.下列各有理式哪些是整式?哪些是分式?$\frac{{a}^{2}-ab{-b}^{2}}{a-b}$,$\frac{1}{4}$x2-2xy2,$\frac{2x}{3}$,$\frac{x+1}{3x}$,-4xy,$\frac{1}{5+a}$,$\frac{1}{3}$x+$\frac{1}{2}y$,$\frac{x}{π-3}$
整式:$\frac{1}{4}$x2-2xy2,$\frac{2x}{3}$,-4xy,$\frac{1}{3}$x+$\frac{1}{2}y$,$\frac{x}{π-3}$
分式:$\frac{{a}^{2}-ab{-b}^{2}}{a-b}$,$\frac{1}{5+a}$.
分析 判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解答 解:$\frac{1}{4}$x2-2xy2,$\frac{2x}{3}$,-4xy,$\frac{1}{3}$x+$\frac{1}{2}y$,$\frac{x}{π-3}$的分母中均不含有字母,因此它们是整式,而不是分式.$\frac{{a}^{2}-ab{-b}^{2}}{a-b}$,$\frac{1}{5+a}$分母中含有字母,因此是分式.
故答案为:$\frac{1}{4}$x2-2xy2,$\frac{2x}{3}$,-4xy,$\frac{1}{3}$x+$\frac{1}{2}y$,$\frac{x}{π-3}$;$\frac{{a}^{2}-ab{-b}^{2}}{a-b}$,$\frac{1}{5+a}$.
点评 本题主要考查分式的定义,注意π不是字母,是常数,所以$\frac{x}{π-3}$不是分式,是整式.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
2.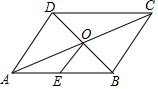 如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
 如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )| A. | 10 | B. | 9 | C. | 8 | D. | 5 |
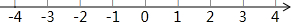 解不等式组$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{2x-1}{3}>\frac{x-1}{2}②}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{2x-1}{3}>\frac{x-1}{2}②}\end{array}\right.$,并把它的解集在数轴上表示出来. .其中x是﹣2、﹣1、0、2中的一个.
.其中x是﹣2、﹣1、0、2中的一个.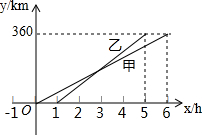 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示. <
<