题目内容
10. 如图,在一个五边形的边AB上有一点O,将O与五边形的顶点C、D、E相连,若∠COB=36°,∠DOE=54°,OC、OE分别平分∠DOB,∠AOD.
如图,在一个五边形的边AB上有一点O,将O与五边形的顶点C、D、E相连,若∠COB=36°,∠DOE=54°,OC、OE分别平分∠DOB,∠AOD.(1)求∠EOC的度数;
(2)写出∠COD的余角和∠AOE的补角;
(3)分别求出∠COD的余角和∠AOE的补角的度数.
分析 (1)根据角平分线的定义求出∠COD的度数,计算即可;
(2)根据余角和补角的概念写出∠COD的余角和∠AOE的补角;
(3)根据余角和补角的概念就进行计算即可.
解答 解:(1)∵OC平分∠DOB,
∴∠COD=∠COB=36°,
∴∠EOC=∠DOE+∠COD=90°;
(2)∠COD的余角是∠DOE和∠AOE,
∠AOE的补角是∠EOB;
(3)∠COD的余角=90°-36°=54°,
∠AOE的补角是180°-54°=126°.
点评 本题考查的是余角和补角的概念,若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补,注意数形结合思想的应用.

练习册系列答案
相关题目
20.已知23×83=2n,则n的值为( )
| A. | 18 | B. | 7 | C. | 8 | D. | 12 |
5.如果点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,那么抛物线的对称轴是( )
| A. | x=3 | B. | x=-3 | C. | x=$\frac{3}{2}$ | D. | x=-$\frac{3}{2}$ |
15.某市已经全面实行了居民新型合作医疗保险制度.享受医保的居民可在规定的医院就医,并按规定标准报销部分医疗费用.下表是医疗费用报销的标准:
若家住幸福社区的王爷爷在一次住院中个人自负住院医疗费5000元(自负医疗费=实际医疗费-按标准报销的金额),则他在这一次住院中的实际医疗费用为多少元?
| 医疗费用范围 | 门诊 | 住院 | ||
| 不超过5000元的部分 | 超过5000元且不超过10000元的部分 | 超过10000元的部分 | ||
| 每年报销比例标准 | 30% | 70% | 80% | 90% |
 列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?
列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?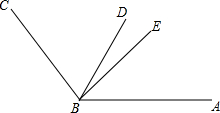 如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.
如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.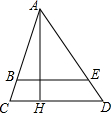 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.