题目内容
5.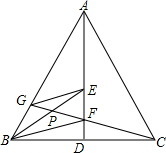 如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证:
如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证:(1)△GBF是等腰三角形;
(2)GE∥BF.
分析 (1)设∠ABE=∠EBF=∠FBC=x,得到∠GBF=2x,由AD是等腰三角形ABC底边上的高,于是得到AD是等腰三角形ABC底边上的垂直平分线,根据线段垂直平分线的性质得到BF=CF,由等腰三角形的性质得到∠FCB=∠FBC=x,求得∠GFB=∠FCB+∠FBC=2x,推出∠GBF=∠GFB,于是求得结论;
(2)延长FD到H,使DH=DF,连接BH,CH,根据AD垂直平分BC,得到四边形BFCH是平行四边形,根据平行四边形的性质得到CF∥BH,求出BF=CF,推出?BFCH是菱形,求得BH=BF,∠HBF=2∠DBF=∠ABF,根据角平分线定理得到$\frac{AE}{EF}=\frac{AB}{BF}$,$\frac{AF}{FH}=\frac{AB}{BH}$,根据平行线分线段成比例定理得到$\frac{AF}{FH}=\frac{AG}{BG}$,等量代换得到$\frac{AE}{EF}=\frac{AG}{BG}$,即可得到结论.
解答 解:(1)设∠ABE=∠EBF=∠FBC=x,
∴∠GBF=2x,
∵AD是等腰三角形ABC底边上的高,
∴AD是等腰三角形ABC底边上的垂直平分线,
∴BF=CF,
∴∠FCB=∠FBC=x,
∴∠GFB=∠FCB+∠FBC=2x,
∴∠GBF=∠GFB,
∴GB=GF,
∴△GBF为等腰三角形;
(2)延长FD到H,使DH=DF,连接BH,CH,
∵AD垂直平分BC,
∴四边形BFCH是平行四边形,
∴CF∥BH,
∵BF=CF,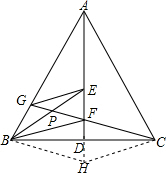 ∴?BFCH是菱形,
∴?BFCH是菱形,
∴BH=BF,∠HBF=2∠DBF=∠ABF,
∵BE平分∠ABF,
根据角平分线定理得:$\frac{AE}{EF}=\frac{AB}{BF}$,
∵BF平分∠ABH,
根据角平分线定理得:$\frac{AF}{FH}=\frac{AB}{BH}$,
∵GF∥BH,
∴$\frac{AF}{FH}=\frac{AG}{BG}$,
∴$\frac{AE}{EF}=\frac{AG}{BG}$,
∴GE∥BF.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,角平分线定理,平行线分线段成比例定理,掌握的作出辅助线是解题的关键.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )
如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )| A. | $\frac{{a}^{2}}{6}$ | B. | $\frac{{a}^{2}}{5}$ | C. | $\frac{{a}^{2}}{4}$ | D. | $\frac{{a}^{2}}{3}$ |
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
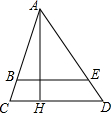 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.