题目内容
11.若5+$\sqrt{11}$的小数部分为a,5-$\sqrt{11}$的小数部分为b,求a+b.解:因为3<$\sqrt{11}$<4,所以5+$\sqrt{11}$的整数部分为8,5-$\sqrt{11}$的整数部分为1.则5+$\sqrt{11}$的小数部分a=5+$\sqrt{11}$-8=$\sqrt{11}$-3,5-$\sqrt{11}$的小数部分b=5-$\sqrt{11}$-1=4-$\sqrt{11}$,所以a+b=$\sqrt{11}$-3+4-$\sqrt{11}$=1.
阅读后,请解答下列问题:
若6+$\sqrt{10}$的整数部分为a,小数部分为b,求2a-($\sqrt{10}$+3)b+2015的值.
分析 利用完全平方数得到3<$\sqrt{10}$<16,则可判断6+$\sqrt{10}$的整数部分为9,所以6+$\sqrt{10}$的小数部分为$\sqrt{10}$-3,即a=9,b=$\sqrt{10}$-3,然后把a、b的值代入2a-($\sqrt{10}$+3)b+2015中利用平方差公式计算.
解答 解:因为3<$\sqrt{10}$<16,所以6+$\sqrt{10}$的整数部分为9,6+$\sqrt{10}$的小数部分为6+$\sqrt{10}$-9=$\sqrt{10}$-3,
即a=9,b=$\sqrt{10}$-3,
所以2a-($\sqrt{10}$+3)b+2015=2×9-($\sqrt{10}$+3)($\sqrt{10}$-3)+2015
=18-(10-9)+2015
=2032.
点评 本题考查了无理数的估算:解题关键是确定无理数的整数部分即可解决问题.

练习册系列答案
相关题目
18.化简a-[b-2a-(a-b)]的结果是( )
| A. | -2a | B. | 2a | C. | 4a-2b | D. | 2a-2b |
 列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?
列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?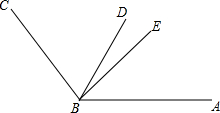 如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.
如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数. 如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O直径,切线CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,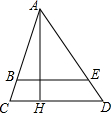 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.