题目内容
2. 用18m长的铝合金型材做一个形状如图所示的矩形窗框.做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用18m长的铝合金型材做一个形状如图所示的矩形窗框.做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
分析 设窗的高度为xm,宽为为为$\frac{18-2x}{4}$m,则根据矩形面积公式列出二次函数,求函数值的最大值即可.
解答 解:设窗框的长为x,
∴宽为$\frac{18-2x}{4}$,
∴y=$\frac{18-2x}{4}$x,
即y=-$\frac{1}{2}$x2+$\frac{9}{2}$x,
∵-$\frac{1}{2}$<0
∴y有最大值,即:当x=-$\frac{\frac{9}{2}}{2×(-\frac{1}{2})}$=4.5m时
y最大=$\frac{4ac-{b}^{2}}{4a}$=$\frac{-\frac{81}{4}}{4×(-\frac{1}{2})}$=10.125m2,
$\frac{18-2×\frac{9}{2}}{4}$=$\frac{9}{4}$m,
∴做成长、宽各为4.5m,$\frac{9}{4}$m时,才能使做成的窗框的透光面积最大,最大透光面积是10.125m2.
点评 本题考查了二次函数的应用,熟记二次函数的顶点坐标公式是解题的关键.

练习册系列答案
相关题目
15.某市已经全面实行了居民新型合作医疗保险制度.享受医保的居民可在规定的医院就医,并按规定标准报销部分医疗费用.下表是医疗费用报销的标准:
若家住幸福社区的王爷爷在一次住院中个人自负住院医疗费5000元(自负医疗费=实际医疗费-按标准报销的金额),则他在这一次住院中的实际医疗费用为多少元?
| 医疗费用范围 | 门诊 | 住院 | ||
| 不超过5000元的部分 | 超过5000元且不超过10000元的部分 | 超过10000元的部分 | ||
| 每年报销比例标准 | 30% | 70% | 80% | 90% |
10. 如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )
如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )
 如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )
如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )| A. | $\frac{{a}^{2}}{6}$ | B. | $\frac{{a}^{2}}{5}$ | C. | $\frac{{a}^{2}}{4}$ | D. | $\frac{{a}^{2}}{3}$ |
14.10件衬衣中,有2个不合格,现从中任意抽取1件进行检测,抽到不合格衬衣的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
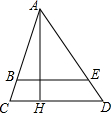 如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.
如图,△ACD中,AH是高,BE∥CD,如果AB=4cm,BC=1cm,AE=6cm,BE=4.8cm.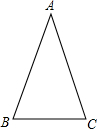 已知:如图,△ABC中,AB=AC.
已知:如图,△ABC中,AB=AC.