题目内容
6.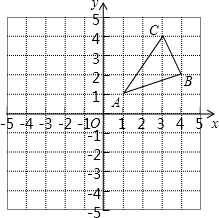 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移4个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在y轴上找一点P,使PA+PC的值最小,请直接写出P的坐标.
分析 (1)依据平移的方向和距离确定出A、B、C的对应的点的坐标;
(2)依据关于原点对称点的坐标特点可确定出点A、B、C关于原点对称点的坐标;
(3)找出A的对称点A′(-1,1),连接CA′,与y轴交点即为P,然后利用待定系数法求得直线A′C的解析式即可.
解答 解:(1)如图1所示:
(2)如图2所示:
(3)找出A的对称点A′(-1,1),连接CA′,与y轴交点即为P.
设直线A′C的解析式为y=kx+b,将点A′和点C的坐标代入得:$\left\{\begin{array}{l}{-k+b=1}\\{3k+b=4}\end{array}\right.$,
①×3+②得:4b=7,解得b=$\frac{7}{4}$.
所以点P坐标为(0,$\frac{7}{4}$).
点评 本题主要考查的是利用平移变换、旋转变换作图、轴对称路径最短问题,利用待定系数法求得b的值是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.某校八年级学生去距学校10km的科技馆参观,一部分学生骑自行车,过了30min,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑自行车学生速度的4倍,设骑自行车学生的速度为xkm/h,则下列方程正确的是( )
| A. | $\frac{10}{x}$=$\frac{10}{4x}$$+\frac{1}{2}$ | B. | $\frac{10}{x}$=$\frac{10}{4x}$-30 | C. | $\frac{10}{x}$=$\frac{10}{4x}$-$\frac{1}{2}$ | D. | $\frac{10}{x}$=$\frac{10}{4x}$+30 |
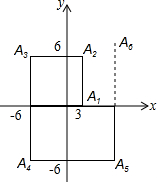 如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时坐标是(9,12),A2013时坐标是(3021,-3018).
如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时坐标是(9,12),A2013时坐标是(3021,-3018).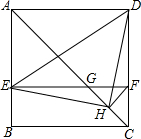 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
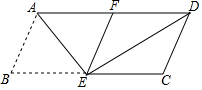 如图,将?ABCD沿过点A的直线折叠,使点B落到AD边上的点F处,折痕为AE,连接FE、DE.
如图,将?ABCD沿过点A的直线折叠,使点B落到AD边上的点F处,折痕为AE,连接FE、DE. 如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,则不等式kx+b<-2x的解集为x<-1.
如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,则不等式kx+b<-2x的解集为x<-1.