题目内容
17.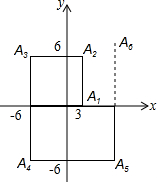 如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时坐标是(9,12),A2013时坐标是(3021,-3018).
如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时坐标是(9,12),A2013时坐标是(3021,-3018).
分析 由于一个机器人从O点出发,向正东方向走3m,到达A1点,那么A1点坐标为(3,0),再向正北走6m到达A2点,那么A2点坐标为(3,6),再向正西走9m到达A3点,那么A3点坐标为(-6,6),然后依此类推,找出规律,即可求出A6的坐标以及A2013的坐标.
解答  解:根据题意可知:OA1=3,A1A2=6,A2A3=9,A3A4=12,A4A5=15,A5A6=18,
解:根据题意可知:OA1=3,A1A2=6,A2A3=9,A3A4=12,A4A5=15,A5A6=18,
∴A1点坐标为(3,0),
A2点坐标为(3,6),
A3点坐标为(-6,6),
A4点坐标为(-6,-6),
A5点坐标为(9,-6),
A6点坐标为(9,12),
以此类推,A9点坐标为(15,-12),A13点坐标为(21,-18),
∵A2在第一象限,而(2013-1)÷4=503,
∴A2013在第四象限,
又∵A5(9,-6),A9(15,-12),A13(21,-18)都在第四象限,
∴落在第四象限内的点每走动4次,横坐标增加6,
∴A2013的横坐标为:3+503×6=3021,纵坐标为-3021+3=-3018,
∴A2013点坐标是(3021,-3018).
故答案为:(9,12),(3021,-3018).
点评 本题主要考查了坐标确定位置的运用,解题的关键是发现规律,利用规律解决问题,解题时注意:各象限内点P(a,b)的坐标特征为:①第一象限:a>0,b>0;②第二象限:a<0,b>0;③第三象限:a<0,b<0;④第四象限:a>0,b<0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.如果不等式3x-m≤0的正整数解为1,2,3,则m的取值范围为( )
| A. | m≤9 | B. | m<12 | C. | m≥9 | D. | 9≤m<12 |
 如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )
如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )



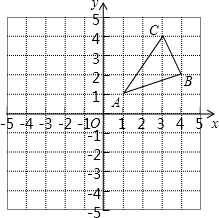 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).