题目内容
15.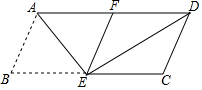 如图,将?ABCD沿过点A的直线折叠,使点B落到AD边上的点F处,折痕为AE,连接FE、DE.
如图,将?ABCD沿过点A的直线折叠,使点B落到AD边上的点F处,折痕为AE,连接FE、DE.(1)求证:四边形ABEF是菱形;
(2)若DE平分∠ADC,四边形CDFE会是菱形吗?请说明理由.
分析 (1)由折叠的性质知,∠1=∠2,AB=AF,由平行四边形的性质得到AD∥BC,AD=BC,于是有∠2=∠3,进而得到∠1=∠3,根据等腰三角形的判定证得AB=BE,即可得到AF=BE,由于AF∥BE,即可证得结论;
(2)由线段的和差关系得到DF=CE,易证四边形CDFE是平行四边形,由∠4=∠5,∠4=∠6,得到∠5=∠6,根据等腰三角形的判定得到CD=CE,由菱形的判定即的结论.
解答 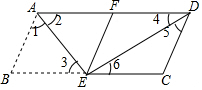 证明:(1)由折叠知,∠1=∠2,AB=AF,
证明:(1)由折叠知,∠1=∠2,AB=AF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠2=∠3,
∴∠1=∠3,
∴AB=BE,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是菱形;
(2)四边形CDFE会是菱形,
∵AD-AF=BC-BE,即DF=CE,DF∥CE,
∴四边形CDFE是平行四边形,
∵DE平分∠ADC,
∴∠4=∠5,
∵AD∥BC,
∴∠4=∠6,
∴∠5=∠6,
∴CD=CE,
∴?CDFE是菱形.
点评 本题考查了平行四边形的性质,折叠的性质,等腰三角形的判定与性质,菱形的判定和性质,根据折叠的性质证得AB=BE是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5.下列运算中,错误的是( )
①$\sqrt{1\frac{25}{144}}$=1$\frac{5}{12}$,②$\sqrt{(-4)^{2}}$=-4,③$\sqrt{-1}$=-$\sqrt{1}$,④($\sqrt{\frac{1}{16}}$)2=$\frac{1}{4}$.
①$\sqrt{1\frac{25}{144}}$=1$\frac{5}{12}$,②$\sqrt{(-4)^{2}}$=-4,③$\sqrt{-1}$=-$\sqrt{1}$,④($\sqrt{\frac{1}{16}}$)2=$\frac{1}{4}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.一个正多边形的内角和等于外交和的5倍,这个正多边形的边数为( )
| A. | 8 | B. | 10 | C. | 11 | D. | 12 |
5.若一个数的立方根恰好于它的平方根相等,则这个数一定是( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | -1或0或1 |
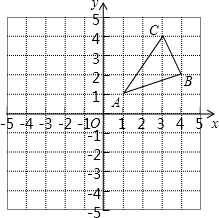 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).