题目内容
11.先阅读理解下面的例题,再按要求解答下列问题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
求代数式m2+m+1的最小值.
分析 把所求代数式写成完全平方的形式,再根据非负数的性质求解即可.
解答 解:m2+m+1=m2+m+$\frac{1}{4}$+$\frac{3}{4}$=(m+$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,
所以m2+m+1的最小值是$\frac{3}{4}$.
点评 本题考查了配方法的应用,非负数的性质,完全平方公式,熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
相关题目
19.式子$\sqrt{2}$的值( )
| A. | 在0到1之间 | B. | 在1到2之间 | C. | 在2到3之间 | D. | 等于4 |
3.一个正多边形的内角和等于外交和的5倍,这个正多边形的边数为( )
| A. | 8 | B. | 10 | C. | 11 | D. | 12 |
 如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )
如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )



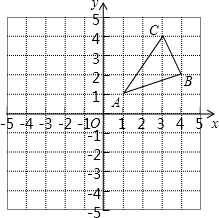 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).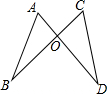 如图,线段AD、BC相交于点O,连接AB、CD.下列条件:①AB=CD,AO=CO;②∠A=∠C,AO=CO;③AO=CO,BO=DO;④∠B=∠D,AB=CD;⑤∠B=∠D,∠A=∠C;从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$.
如图,线段AD、BC相交于点O,连接AB、CD.下列条件:①AB=CD,AO=CO;②∠A=∠C,AO=CO;③AO=CO,BO=DO;④∠B=∠D,AB=CD;⑤∠B=∠D,∠A=∠C;从中任选一组能得出△ABO≌△CDO的概率是$\frac{3}{5}$. 如图,小明要测量水池的宽AB,但没有足够长的绳子,聪明的他想了如下办法:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,则DE的长度就是AB的长,理由是根据边角边(或SAS)(用简写形式即可),可以得到△ABC≌△DCE,从而由全等三角形的对应边相等得出结论.
如图,小明要测量水池的宽AB,但没有足够长的绳子,聪明的他想了如下办法:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,则DE的长度就是AB的长,理由是根据边角边(或SAS)(用简写形式即可),可以得到△ABC≌△DCE,从而由全等三角形的对应边相等得出结论.