题目内容
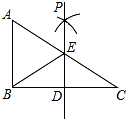 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=| 1 |
| 2 |
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
考点:作图—基本作图,线段垂直平分线的性质
专题:
分析:(1)由作图可得出直线ED为线段BC的中垂线,即可得出①ED⊥BC正确;
(2)由直角三角形斜边中线相等可得AE=BE,∠A=∠EBA;故②正确;
(3)利用假设法证明得出△ABE为等边三角形与△ABE为等腰三角形矛盾.故③错误;
(4)利用ED是△ABC的中位线可得ED=
AB,故④正确.
(2)由直角三角形斜边中线相等可得AE=BE,∠A=∠EBA;故②正确;
(3)利用假设法证明得出△ABE为等边三角形与△ABE为等腰三角形矛盾.故③错误;
(4)利用ED是△ABC的中位线可得ED=
| 1 |
| 2 |
解答:解:由题意可得直线ED为线段BC的中垂线,
∴ED⊥BC;故①正确;
∵∠ABC=90°,ED⊥BC;
∴DE∥AB,
∵点D是BC边的中点,
∴点E为线段AC的中点,
∴AE=BE,
∴∠A=∠EBA;故②正确;
如果EB平分∠AED;
∵∠A=∠EBA,DE∥AB,
∴∠A=∠EBA=∠AEB,
∴△ABE为等边三角形.
∵△ABE为等腰三角形.故③错误;
∵点D是BC边的中点,点E为线段AC的中点,
∴ED是△ABC的中位线,
∴ED=
AB,故④正确.
故选:B.
∴ED⊥BC;故①正确;
∵∠ABC=90°,ED⊥BC;
∴DE∥AB,
∵点D是BC边的中点,
∴点E为线段AC的中点,
∴AE=BE,
∴∠A=∠EBA;故②正确;
如果EB平分∠AED;
∵∠A=∠EBA,DE∥AB,
∴∠A=∠EBA=∠AEB,
∴△ABE为等边三角形.
∵△ABE为等腰三角形.故③错误;
∵点D是BC边的中点,点E为线段AC的中点,
∴ED是△ABC的中位线,
∴ED=
| 1 |
| 2 |
故选:B.
点评:本题主要考查了基本作图及线段的垂直平分线,解题的关键是确定ED是为线段BC的中垂线.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
下列条件中,不能判定△ABC≌△A1B1C1的是( )
| A、AB=A1B1,∠A=∠A1,AC=A1C1 |
| B、AB=A1B1,BC=B1C1,AC=A1C1 |
| C、AB=A1B1,∠B=∠B1,∠C=∠C1 |
| D、AC=A1C1,AB=A1B1,∠B=∠B1 |
 如图,⊙I是△ABC的内切圆,求∠BIC的度数y(度)与∠A的度数x(度)的函数关系式.
如图,⊙I是△ABC的内切圆,求∠BIC的度数y(度)与∠A的度数x(度)的函数关系式.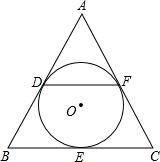 如图,△ABC的内切圆⊙O分别和AB,BC,CA切于点D,E,F,∠A=60°,BC=6,△ABC的周长为18,则DF的长为
如图,△ABC的内切圆⊙O分别和AB,BC,CA切于点D,E,F,∠A=60°,BC=6,△ABC的周长为18,则DF的长为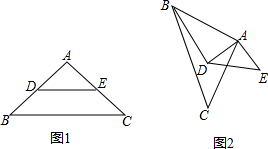 已知在△ABC中,AB=AC,DE分别是AB,AC的中点,将ABC绕点A顺时针旋转a角(0°<a<180°),得到AB′C′,(如图2),探究DB′与EC′的数量关系,并加以证明.
已知在△ABC中,AB=AC,DE分别是AB,AC的中点,将ABC绕点A顺时针旋转a角(0°<a<180°),得到AB′C′,(如图2),探究DB′与EC′的数量关系,并加以证明.