题目内容
 如图,⊙I是△ABC的内切圆,求∠BIC的度数y(度)与∠A的度数x(度)的函数关系式.
如图,⊙I是△ABC的内切圆,求∠BIC的度数y(度)与∠A的度数x(度)的函数关系式.考点:三角形的内切圆与内心
专题:
分析:由三角形内角和定理得∠ABC+∠ACB=180°-∠A,∠ABC与∠ACB的平分线交于点I,则∠IBC+∠ICB=
∠ABC+
∠ACB=
(∠ABC+∠ACB)=
(180°-∠A),在△IBC中,利用三角形内角和定理求∠BIC即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:y=90°+
x°,
理由如下:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵BI、CI是△ABC内角的平分线,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠IBC+∠ICB=
∠ABC+
∠ACB=
(∠ABC+∠ACB)=
(180°-∠A),
在△IBC中,
∠BIC=180°-(∠IBC+∠ICB)=180°-
(180°-∠A)=90°+
∠A
∴∠BIC=90°+
∠A,
即y=90°+
x°.
| 1 |
| 2 |
理由如下:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵BI、CI是△ABC内角的平分线,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠IBC+∠ICB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△IBC中,
∠BIC=180°-(∠IBC+∠ICB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BIC=90°+
| 1 |
| 2 |
即y=90°+
| 1 |
| 2 |
点评:本题主要考查了三角形的内心的计算,正确理解∠IBC+∠ICB=
(∠ABC+∠ACB)是关键.
| 1 |
| 2 |

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||||||
| B、|3.14-π|=π-3.14 | ||||||
C、
| ||||||
D、
|
在Rt△ABC中,∠C=90°,sinA=
.则cosB的值为( )
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,求∠BAC的度数.
如图,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,求∠BAC的度数.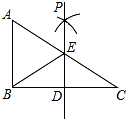 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= 如图,已知线段AB=10cm,C是线段AB上一点,D是线段AC的中点,E是线段BC的中点,则DE的长是
如图,已知线段AB=10cm,C是线段AB上一点,D是线段AC的中点,E是线段BC的中点,则DE的长是