题目内容
9.已知x、y满足方程组$\left\{\begin{array}{l}{x+2y=12}\\{2x+y=-15}\end{array}\right.$,求(x+y)2013的值.分析 运用代入消元法解出方程组,求出x、y的值,根据乘方的概念计算即可.
解答 解:$\left\{\begin{array}{l}{x+2y=12①}\\{2x+y=-15②}\end{array}\right.$,
由①得,x=12-2y③,
把③代入②得,y=13,
把y=13代入③得,x=-14,
则方程组的解是$\left\{\begin{array}{l}{x=-14}\\{y=13}\end{array}\right.$,
(x+y)2013=-1.
点评 本题考查的是二元一次方程组的解法和乘方的运算,代入法解二元一次方程组的一般步骤:①从方程组中选一个系数比较简单的方程,将这个方程组中的一个未知数用含另一个未知数的代数式表示出来.②将变形后的关系式代入另一个方程,消去一个未知数,得到一个一元一次方程.③解这个一元一次方程,求出x(或y)的值.④将求得的未知数的值代入变形后的关系式中,求出另一个未知数的值.

练习册系列答案
相关题目
19.一根钢筋三脚架的三边分别为20cm,50cm,60cm,现要做一个与其相似的钢筋三脚架,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为另外两边,则不同的截法有( )
| A. | 一种 | B. | 两种 | C. | 三种 | D. | 五种 |
1.解方程$\frac{5}{9}$($\frac{9}{5}$x+1)=1,下列变形最简单的是( )
| A. | 方程两边同时乘以9,得5($\frac{9}{5}$x+1)=9 | B. | 方程两边同时乘$\frac{9}{5}$,得$\frac{9}{5}$x+1=$\frac{9}{5}$ | ||
| C. | 去括号,得x+$\frac{5}{9}$=1 | D. | 括号内先通分,得$\frac{5}{9}$×$\frac{9x+5}{5}$=1 |
18.把代数式ax2-4ax+4a分解因式,下列结果中正确的是( )
| A. | a(x-2)2 | B. | a(x+2)2 | C. | a(x-4)2 | D. | a(x-2)(x+2) |
 如图,公园里设计了曲折迂回的九曲桥,与修一座笔直的桥相比,这样做是否增加了游人在桥上行走的路程?说出其中的道理.
如图,公园里设计了曲折迂回的九曲桥,与修一座笔直的桥相比,这样做是否增加了游人在桥上行走的路程?说出其中的道理.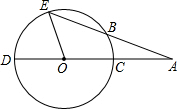 CD是⊙O的直径,AE交⊙O于点B,且AB=OC,∠A=25°,求∠EOD的度数.
CD是⊙O的直径,AE交⊙O于点B,且AB=OC,∠A=25°,求∠EOD的度数.