题目内容
17.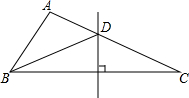 如图,△ABC中,∠A=100°,BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,则∠C的度数等于24°.
如图,△ABC中,∠A=100°,BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,则∠C的度数等于24°.
分析 设∠ABD为4x,∠DBC为3x,利用线段垂直平分线得出∠C为3x,再利用三角形内角和解答即可.
解答 解:∵BC的垂直平分线交AC于点D,且∠ABD:∠DBC=4:3,
∴DC=BD,
∴∠C=∠DBC,
设∠ABD为4x,∠DBC为3x,∠C为3x,
可得:100°+4x+3x+3x=180°,
解得:x=8,
所以∠C=24°.
故答案为:24°.
点评 本题考查的是线段垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
9.已知x+y=8,xy=5,则x2+y2的值是( )
| A. | 84 | B. | 74 | C. | 64 | D. | 54 |
6.若x<0,则化简$\sqrt{{-x}^{3}y}$的结果是( )
| A. | -x$\sqrt{xy}$ | B. | x$\sqrt{-xy}$ | C. | -x$\sqrt{-xy}$ | D. | x$\sqrt{xy}$ |
7.在一个直角三角形中,若其中两边长分别为5cm,3cm,则第三边长为( )
| A. | 4cm | B. | 4cm或$\sqrt{34}$cm | C. | $\sqrt{34}$cm | D. | 不存在 |
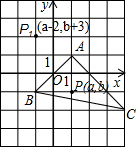 如图所示,三角形ABC中,任意一点P(a,b)经平移后对应点P(a-2,b+3),将△ABC作同样的平移得到△A1B1C1.
如图所示,三角形ABC中,任意一点P(a,b)经平移后对应点P(a-2,b+3),将△ABC作同样的平移得到△A1B1C1. 如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.
如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.